CS231N-损失函数和梯度下降

2023-06-12

字数统计: 1.8k字 | 阅读时长≈ 6分

损失函数与梯度下降

损失函数

SVM loss（Hinge loss）

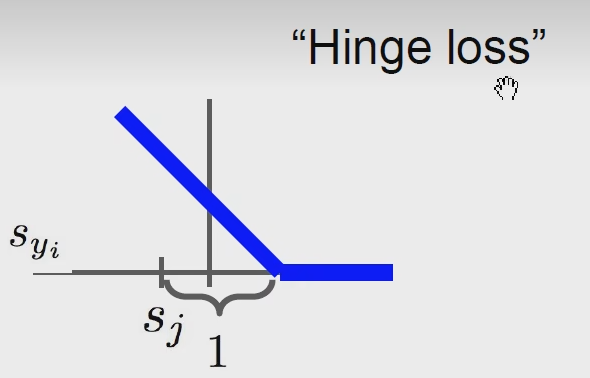
这是一种常在SVM中用的损失函数，SVM是机器学习的基础知识，后面有时间会更新机器学习相关的知识，SVM用我们国学思想来说就是：“中庸之道”，现在大街上一群人，一坨是老师，一坨是学生，用一个线性模型把他们分开，就要找到这两个类之间中间最大安全距离的点，这个中就是中庸之道的中，SVM就是要找到这个最大安全边距的点，它的损失函数就是这种铰链损失函数：

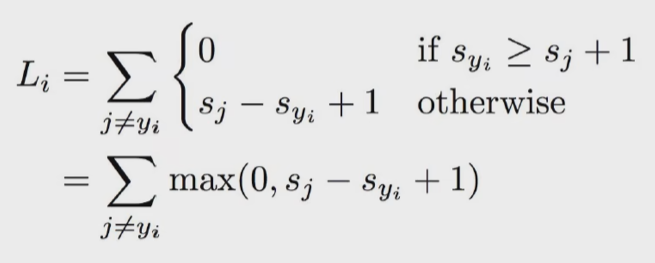
它的数学意义就是对每一个数据把它 分类错误的分数 - 正确类别的分数 + 1 求得这个数和 0 比大小，取最大值，就是这个样本的铰链损失函数。

比如说这个猫：

比如说这个汽车：

比如说这个青蛙：

那我们进一步思考一下，这个铰链损失函数在干嘛，以汽车为例，汽车的得分是4.9，那么铰链损失函数就会去惩罚得分大于3.9的类别，对于得分小于3.9的类别，铰链函数是不会去惩罚它的。

最后求一个平均值，就得到了这个数据集的损失值。

铰链损失函数会惩罚哪些和正确类别得分相近的类别，对于相差较远的，就不会去惩罚它，这里的1，可以看做冗余的安全度。

平方铰链损失函数

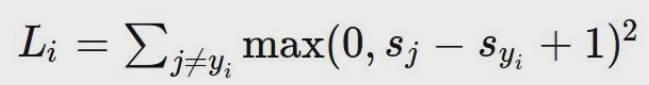
这个损失函数和普通的损失函数大小是对应的，只不过这个函数会放大损失得分很高的类别，也就是告诉我们要去重点优化差距特别大的那些分类，这两个损失函数是可以相互替换的。

python实现

import numpy as np
def L_i_vectorized(x,y,W):
    # scores 是数据集的得分矩阵
    # 假设某一个数据集上有50000张图片，每一个图片都是10分类，那么scores就是50000行 10列
    scores = W.dot(x)  # 每一张图片的分时
    margins = np.maximum(0,scores - scores[y] + 1) # 每一行都减去对应正确类别的分数 + 1
    margins[y] = 0 # 指定正确类别的损失函数为 0
    loss_i = np.sum(margins) # 求和
    return loss_i

这个损失函数是不受权重影响的，同一个损失函数可以对应好多套权重，本着越简单越好的原则，选择数比较小的权重比较好，这里就要引入一个很重要的理论，正则化，regularization。

regularization

在损失函数后加了一个正则化项

正则化就是让这个模型更加简单，让这个参数和权重更加小，可以在测试集上更好的泛化。

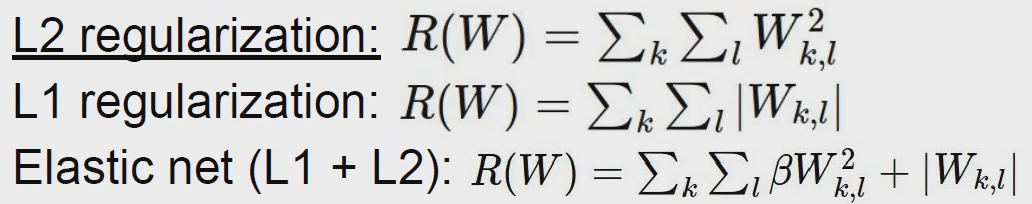
有L1正则化和L2正则化。

举个栗子

x是输入的四个维度的特征，w1和w2是两个权重，他们的损失分数都是1，但是选哪个好呢？

选第二个好，因为第一个出现了一家独大的情况，很容易出现过拟合的情况，第二个则是雨露均沾。

在多项式回归也会用到正则化，如下图：

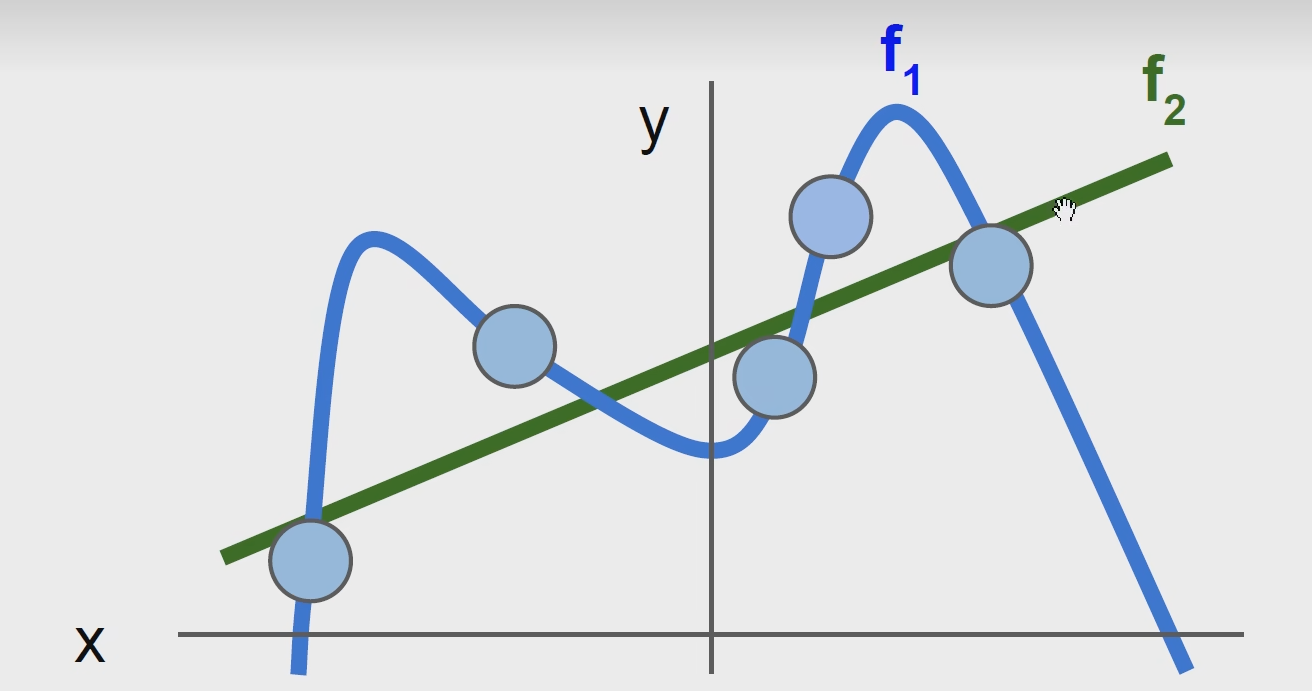
这两个回归拟合模型用那个？肯定用绿色的，蓝色的模型死记硬背了一些噪声点，把这个模型变得十分复杂，用多项式函数来拟合这个模型的话会发现它的高次项是非常大的，而直线就是kx + b的形式，通过正则化把蓝色的惩罚掉就可以，避免过拟合，寻找大而化之的边界线。

Softmax Classifier 多分类的逻辑回归

我们得到了每个分类的得分，我们想要吧得分去变成每一个类别的概率，但是这里还有很讨厌的负数，这要怎么搞？

首先我们使用一个指数函数：

之后对这些数进行归一化：

那么经过这样变换的叫做概率，这个变换，就叫做Softmax，它的作用就是把分数变成了概率。

这里我们就要引入一个新的损失函数：

交叉熵损失函数

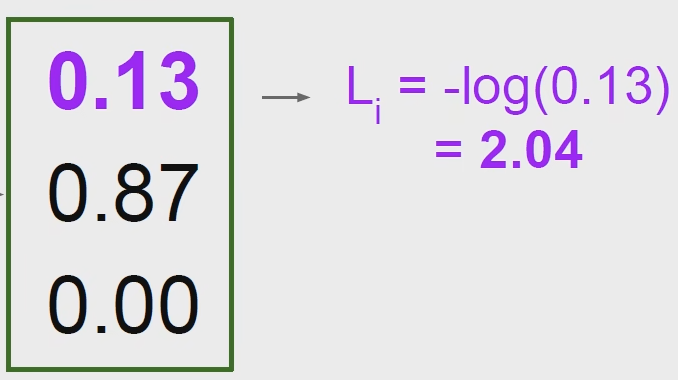
可以想象一个-log的曲线，如果这个正确的概率越接近1，那么它的损失函数值就越接近0，这样就很好进行模型的衡量，此时我们只关心分类正确的情况，也叫最大似然估计可以去看一下（CS229 机器学习的内容）

选用log这个函数真的十分巧妙，它可以吧乘积变成求和，这样就方便我们统计整个数据集分类正确的得分。

优化过程梯度下降

一种思想是随机权重，最后选取一个效果最好的权重，类似量化投资里的羊驼投资法（挺抽象的）

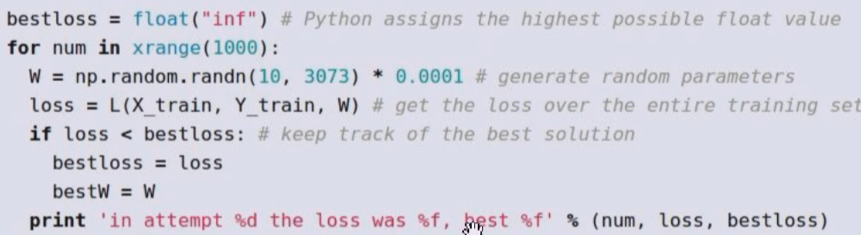
这种竟然还有15.5%的准确率，比随机猜的准确率也高，也不失为一种方法

另外一种比较靠谱的方法就是求导，现在要降低损失率，也就是下山，通过求导，就知道哪里的坡度最大，顺着坡度最大的地方下山就可以。导数告诉我们的是上山最快的方向，所以现在需要加一个负号。将损失函数对每一个权重求偏导，然后找到各个参数应该变化的方向，找到最大的，加个负号，返回去影响权重，就可以使损失率快速下降。

在这里加一个很小的数，然后近似求一个导数，就可以得到结果，这是一个比较暴力无脑的办法，这个方法比较慢，需要遍历每一个权重，而且求得是近似值，好处就是容易编程实现。

所以，可以直接使用求导公式去求。

while True:
    weights_grad = evaluate_grandient(loss_fun, data, weights) # 梯度
    weights += - step_size * weights_grad
    # step_size  这里乘的是一个学习率，为的是不让它快速下山
    # 如果学习率比较小  那么就是小碎步下山

梯度下降的下降是使得损失函数下降，而不是梯度本身下降！

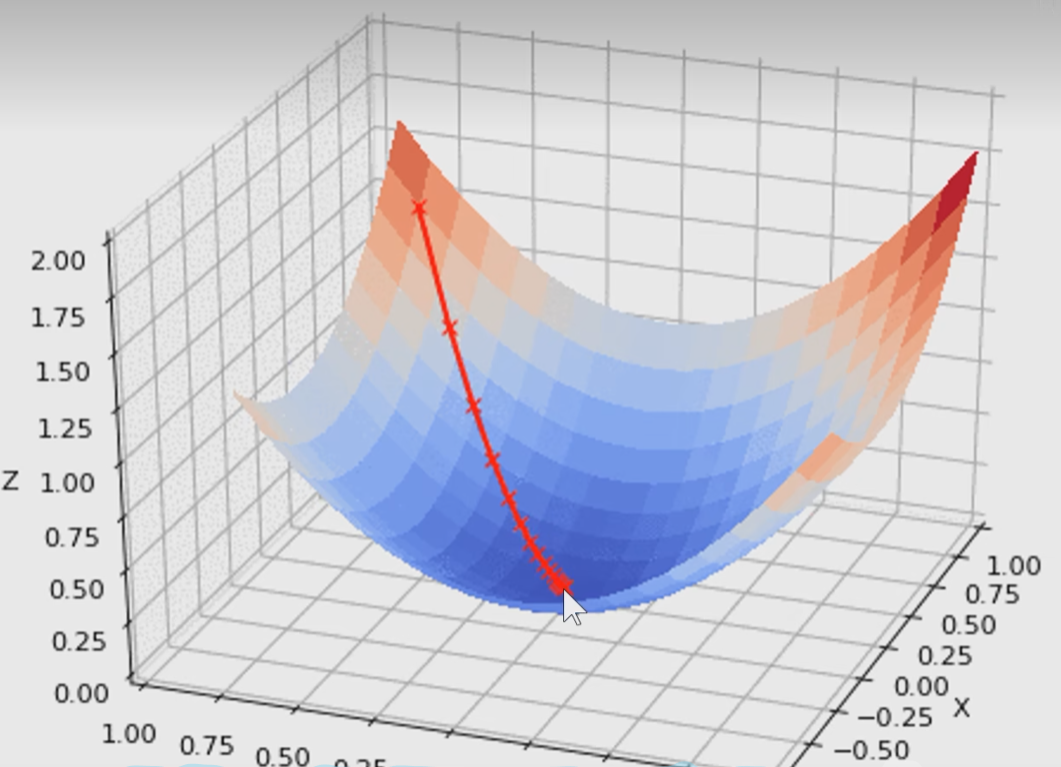
有的时候数据量比较大，可能达到几千万张图片，这个时候全部算一次是十分不经济的，可以一口一口的喂进去

while True:
    data_batch = sample_training_data(data,256)
    weights_grad = evaluate_grandient(loss_fun, data, weights) # 梯度
    weights += - step_size * weights_grad
    # step_size  这里乘的是一个学习率，为的是不让它快速下山
    # 如果学习率比较小  那么就是小碎步下山

这里的 256 就是 mini batch

这256是不具有代表性的，它更新的时候就像一个醉汉一样，摇摇摆摆，有的时候会升高有的时候会降低，但是，道路是曲折的，前途是光明的，最终肯定还是可以收敛到一个比较好的效果的。

本文作者： 李宝璐
本文链接： https://libaolu312.github.io/2023/06/12/CS231N-线性分类、损失函数和梯度下降/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！