关键路径为起点到终点权值加起来最大的路径

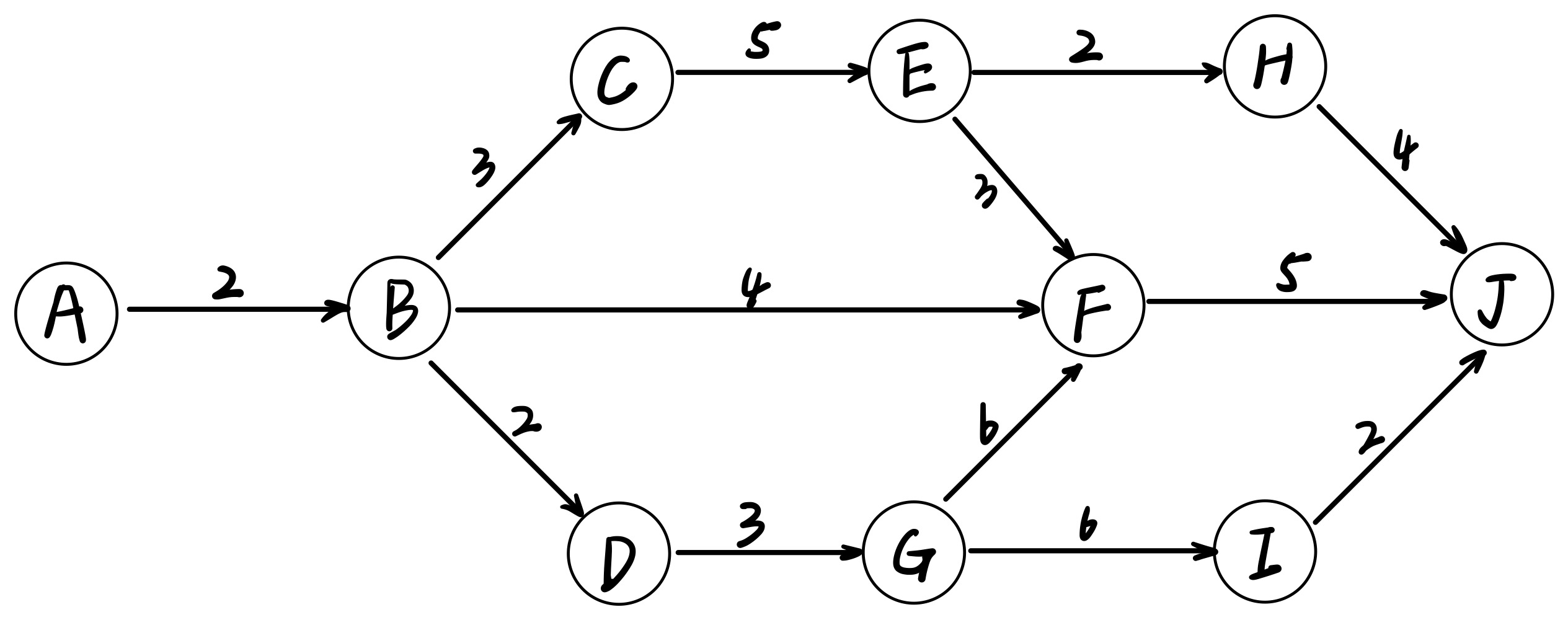
某个项目的活动图如上图所示，其中顶点表示项目里程碑，连接顶点的边表示包含的活动，边上的数字表示相应活动的持续时间（天），则完成该项目的最少时间为 _ 天，活动BC和BF最多可以晚开始 _ 天而不会影响整个项目的进度。

误区

需要注意的是，图中的点，并不代表活动，并不能说活动 A 用 2 天到达活动 B ，这是不准确的，图上的点应该理解为 “里程碑”。如果说到达里程碑 F 的边有三条 E –> F, B –> F, 和 G –> F，意思是有三个活动，完成后到达里程碑 F，并不能说 F 是个活动，如果这么理解会在计算最晚开始时间时出现错误。

首先

关键路径为最大（大）的总值，计算可以得到ABCEFJ=18,所以关键路径的值为18

一、最早开始时间

从起点到该点的最长（大）的值

• A：起点，最早开始时间为0

• B：起点到B只有AB=2

• C：起点到C只有ABC=2+3=5

• D：起点到D只有ABD=2+2=4

• E：起点到E只有ABCE=2+3+5=10

• F：起点到F有ABCEF=13

  ​ ABF=6

  ​ ABDGF=13

  ​ 取最大，其中ABCEF和ABDGF一样值，所以F的最早开始时间为13

• G：ABDG=7

• H：ABCEH=12

• I：ABDGI=13

• J：J有H，F，I 这3个点到J，其中ABCEHJ=12+4=16

  ​ 0到F最大+<F,J>=13+5=18

  ​ 0到I最大+<I,J>=13+2=15

  ​ 取最大，所以J的最早开始时间为18

二、最晚开始时间

关键路径的值 - 终点到该点的最大的值

或者这样理解：关键路径的值 - 终点到该点的值，如果得到的有多个值，那么取最小

MIN { 关键路径的值 - 终点到该点的值 }

为了方便运算，求最晚的都是通过反方向来求的

• J：0

• H：重点到H只有JH，18-4=14

• F：18-5=13

• I：18-2=16

• E：有JFE=8

  ​ JHE=6

  ​ 有最晚开始时间MIN{ 18-8=10，18-6=12 }=10

• G：有JFG=11

  ​ JIG=8

  ​ 最晚开始时间 MIN{ 18-11=7，18-8=10}=7

• C：因为已经求出E了，可以更简单地运算

  ​ E的最晚开始时间 - <C，E>=10-5=5

• D：G的最晚开始时间 - < D,G>=7-3=4

• B：反方向回来的，有C和D两个点到B，则

  ​ BC的方向：C的最晚开始时间 - <B,C>=5-3=2

  ​ DB的方向：D的最晚开始时间 - <B,D>=4-2=2

  ​ 所以B的最晚开始时间为2

三、活动的最长耽搁时间/最晚开始X天不影响整体

活动的最长耽搁时间/最晚开始X天不影响整体=后继点的最晚-前驱点的最早-该活动的值

比如

• 活动BF最长耽搁时间=F的最晚-B的最早 - <B,F>=13-2-4=7
• 活动BC最长耽搁时间=C的最晚-B的最早 - <B,C>=5-2-3=0

其他的也一样，就不写了

四、活动最迟（晚）应该在第X天开始（出发）

活动最迟（晚）应该在第X天开始（出发）：关键路径-前驱点到终点的最小值

或者说max{ 关键路径 - 前驱到终点的值}

活动GI最迟应该在第X天出发？
18-8=10，其中GIJ为 8 ，关键路径为18
GFJ为11，则18-11=7，10与7取最大，则活动GI最迟应该在10天出发

五、松弛时间

松弛时间=关键路径的总时间-包含该任务的关键路径花的时间
还有一种说法不知道对不对，松弛时间=前驱的最晚时间 - 前驱的最早时间

再来一道题吧，我现代企业管理的一道课后习题：

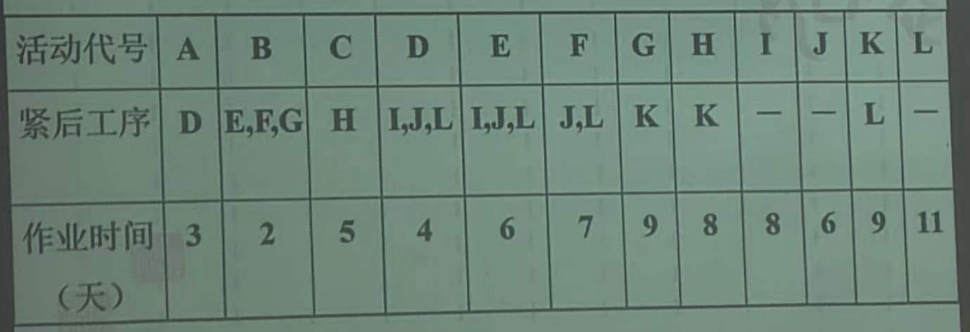
ok，这次我们换个画法吧

这种图叫做AOE图，具体可以去看一些关于数据结构中图结构的资料。

ok，那么就来根据这个表来画这个工程的AOE图吧。

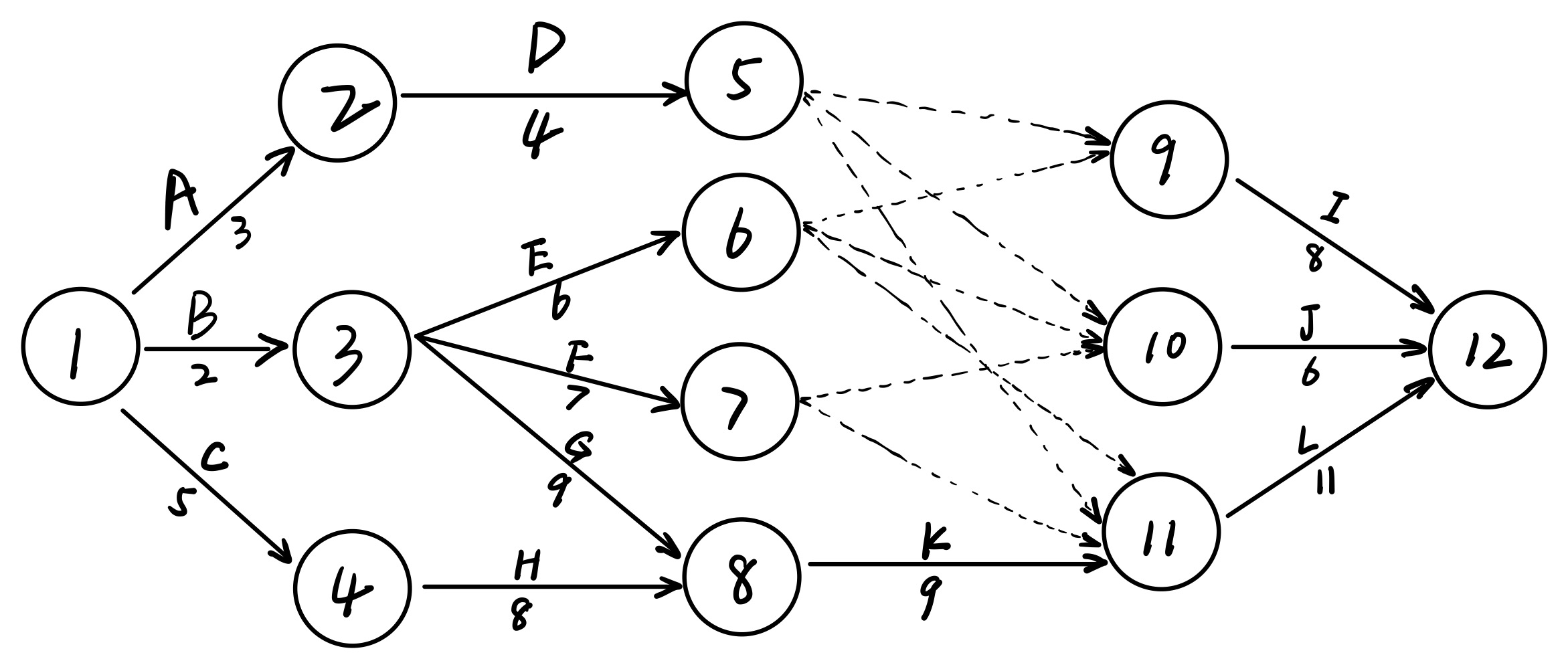
结果如下：