Diffusion Models/Score-based Generative Models背后的深度学习原理（1）:配分函数

2023-11-06

字数统计: 2.1k字 | 阅读时长≈ 7分

Diffusion Models/Score-based Generative Models背后的深度学习原理（1）:配分函数

无向模型

有向图模型为我们提供了一种描述结构化概率模型的语言。而另一种常见的语言则是无向模型(undirected Model)，也被称为马尔可夫随机场(Markov random field, MRF)或者是马尔可夫网络(Markov network)(Kindermann, 1980)。就像它们的名字所说的那样,无向模型中所有的边都是没有方向的。

当存在很明显的理由画出每一个指向特定方向的箭头时，有向模型显然最适用。有向模型中，经常存在我们理解的具有因果关系以及因果关系有明确方向的情况。接力赛的例子就是一个这样的情况。之前运动员的表现会影响后面运动员的完成时间，而后面运动员却不会影响前面运动员的完成时间。
然而并不是所有情况的相互作用都有一个明确的方向关系。当相互的作用并没有本质性的指向，或者是明确的双向相互作用时，使用无向模型更加合适。

作为一个这种情况的例子，假设我们希望对三个二值随机变量建模：你是否生病，你的同事是否生病以及你的室友是否生病。就像在接力赛的例子中所作的简化假设一样，我们可以在这里做一些关于相互作用的简化假设。假设你的室友和同事并不认识，所以他们不太可能直接相互传染一些疾病，比如说感冒。这个事件太过罕见，所以我们不对此事件建模。然而，很有可能其中之一将感冒传染给你，然后通过你再传染给了另一个人。我们通过对你的同事传染给你以及你传染给你的室友建模来对这种间接的从你的同事到你的室友的感冒传染建模。

在这种情况下，你传染给你的室友和你的室友传染给你都是非常容易的，所以模型不存在一个明确的单向箭头。这启发我们使用无向模型。其中随机变量对应着图中的相互作用的结点。与有向模型相同的是，如果在无向模型中的两个结点通过一条边相连接，那么对应这些结点的随机变量相互之间是直接作用的。不同于有向模型，在无向模型中的边是没有方向的，并不与一个条件分布相关联。

我们把对应你健康状况的随机变量记作$h_y$，对应你的室友健康状况的随机变量记作$h_x$ ，你的同事健康的变量记作$h_c$ 。下图表示这种关系。

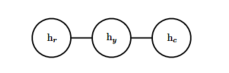
正式地说，一个无向模型是一个定义在无向模型 G上的结构化概率模型。对于图中的每一个团，一个因子（factor）$$ (也称为团势能（clique potential）)，衡量了团中变量每一种可能的联合状态所对应的密切程度。这些因子都被限制为是非负的。它们一起定义了未归一化概率函数： \[ \tilde{p}\left( x \right) =\prod_{c=\varrho}{\phi \left( C \right)} \] 只要所有团中的结点数都不大，那么我们就能够高效地处理这些未归一化概率函数。它包含了这样的思想，密切度越高的状态有越大的概率。然而，不像贝叶斯网络，几乎不存在团定义的结构，所以不能保证把它们乘在一起能够得到一个有效的概率分布。下面展示了一个从无向模型中读取分解信息的例子。

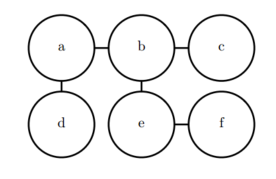
这个图说明通过选择适当的 φ, 函数 p(a; b; c; d; e; f) 可以写作 1 Z φa,b(a; b)φb,c(b; c)φa,d(a; d)φb,e(b; e)φe,f(e; f)。

在你、你的室友和同事之间感冒传染的例子中包含了两个团。一个团包含了$h_y$ 和$h_c$ 。这个团的因子可以通过一个表来定义，可能取到下面的值：状态为1代表了健康的状态，相对的状态为0则表示不好的健康状态（即感染了感冒）。你们两个通常都是健康的，所以对应的状态拥有最高的密切程度。两个人中只有一个人是生病的密切程度是最低的，因为这是一个很罕见的状态。两个人都生病的状态（通过一个人来传染给了另一个人）有一个稍高的密切程度，尽管仍然不及两个人都健康的密切程度。

为了完整地定义这个模型，我们需要对包含$h_y$ 和$h_r$的团定义类似的因子。

配分函数

尽管这个未归一化概率函数处处不为零，我们仍然无法保证它的概率之和或者积分为1。为了得到一个有效的概率分布，我们需要使用对应的归一化的概率分布，一个通过归一化团势能乘积定义的分布也被称作是吉布斯分布： \[ p\left( x \right) =\frac{1}{Z}\tilde{p}\left( x \right) \] 其中，Z是使得所有的概率之和或者积分为1的常数，并且满足： \[ Z=\int{\tilde{p}\left( x \right) dx} \] 当函数p(x)固定时，我们可以把Z当成是一个常数。值得注意的是如果函数p(x)带有参数时，那么Z是这些参数的一个函数。在相关文献中为了节省空间忽略控制Z的变量而直接写Z是一个常用的方式。归一化常数Z被称作是配分函数，这是一个从统计物理学中借鉴的术语。

由于Z通常是由对所有可能的x状态的联合分布空间求和或者求积分得到的，它通常是很难计算的。为了获得一个无向模型的归一化概率分布，模型的结构和函数 $$ 的定义通常需要设计为有助于高效地计算Z。在深度学习中，Z通常是难以处理的。由于Z难以精确地计算出，我们只能使用一些近似的方法。

在设计无向模型时，我们必须牢记在心的一个要点是设定一些使得Z不存在的因子也是有可能的。当模型中的一些变量是连续的，且在其定义域上的积分发散时这种情况就会发生。例如，当我们需要对一个单独的标量变量建模，并且单个团势能在这种情况下： \[ Z=\int{x^2dx} \] 由于这个积分是发散的，所以不存在一个对应着这个势能函数的概率分布。有时候 $$ 函数某些参数的选择可以决定相应的概率分布是否能够被定义。参数$$决定了归一化常数Z是否存在。正的$$使得$$函数是一个关于x的高斯分布，但是非正的参数 $$则使得$$不可能被归一化。

有向建模和无向建模之间一个重要的区别就是有向模型是通过从起始点的概率分布直接定义的，反之无向模型的定义显得更加宽松，通过 $$ 函数转化为概率分布而定义。这改变了我们处理这些建模问题的直觉。当我们处理无向模型时需要牢记一点，每一个变量的定义域对于一系列给定的$$函数所对应的概率分布有着重要的影响。举个例子，我们考虑一个n维向量的随机变量x以及一个由偏置向量b参数化的无向模型。假设x的每一个元素对应着一个团，并且满足$^{( i )}( x_i ) =( b_ix_i ) $。在这种情况下概率分布是怎样的呢？答案是我们无法确定，因为我们并没有指定x的定义域。