Diffusion Models/Score-based Generative Models背后的深度学习原理（2）:基于能量模型和受限玻尔兹曼机

2023-11-06

字数统计: 2.3k字 | 阅读时长≈ 8分

Diffusion Models/Score-based Generative Models背后的深度学习原理（2）:基于能量模型和受限玻尔兹曼机

基于能量模型的定义

无向模型中许多有趣的理论结果都依赖于$\forall x$, $\tilde{p}\left( x \right) >0$这个假设。使这个条件满足的一种简单方式是使用基于能量的模型，其中： \[ \tilde{p}\left( x \right) =\exp \left( -E\left( x \right) \right) \] $E\left( x \right)$ 被称作是能量函数。对所有的 $z$ ， $( z ) $ 都是正的，这保证了没有一个能量函数会使得某一个状态x的概率为0。我们可以完全自由地选择那些能够简化学习过程的能量函数。如果我们直接学习各个团势能，我们需要利用约束优化方法来任意地指定一些特定的最小概率值。学习能量函数的过程中，我们可以采用无约束的优化方法。基于能量的模型中的概率可以无限趋近于0但是永远达不到0。

服从上式形式的任意分布都是玻尔兹曼分布的一个实例。正是基于这个原因，我们把许多基于能量的模型称为玻尔兹曼机。

关于什么时候称之为基于能量的模型，什么时候称之为玻尔兹曼机不存在一个公认的判别标准。一开始玻尔兹曼机这个术语是用来描述一个只有二值变量的模型，但是如今许多模型，比如均值-协方差RBM，也涉及到了实值变量。虽然玻尔兹曼机最初的定义既可以包含潜变量也可以不包含潜变量，但是时至今日玻尔兹曼机这个术语通常用于指拥有潜变量的模型，而没有潜变量的玻尔兹曼机则经常被称为马尔科夫随机场或对数线性模型。

无向模型中的团对应于未归一化概率函数中的因子。通过 $\exp \left( a+b \right) =\exp \left( a \right) +\exp \left( b \right)$ , 我们发现无向模型中的不同团对应于能量函数的不同项。

换句话说，基于能量的模型只是一种特殊的马尔科夫网络：求幂使能量函数中的每个项对用于不同团的一个因子，人们可以将能量函数中的带有多个项的基于能量的模型视作是专家之积。能量函数中的每一项对应的是概率分布中的一个因子。能量函数中的每一项都可以看作决定一个特定的软约束是否能够满足的“专家”。每个专家只执行一个约束，而这个约束仅仅涉及随机变量的一个低维投影，但是当其结合概率的乘法时，专家们一同构造了复杂的高维约束。

基于能量的模型定义的一部分无法用机器学习观点来解释：即“-”符号。这个：“-”符号可以被包含在E的定义之中。对于很多的E函数的选择来说，学习算法可以自由地决定能量的符号。这个负号的存在主要是为了保持机器学习文献和物理学文献之间的兼容性。概率建模的许多研究最初都是由统计物理学家做出的，其中E是指实际的、物理概念的能量，没有任何符号。诸如“能量”和“配分函数”这类术语仍然与这些技术相关联，尽管它们的数学适用性比在物理中更宽。一些机器学习研究者发出了不同的声音，但这些都不是标准惯例。

许多对概率模型进行操作的算法不需要计算 $p_{model}\left( x \right)$ ，而只需计算 $\log \tilde{p}_{model}\left( x \right)$ 。对于具有潜变量h的基于能量的模型，这些算法有时会将该量的负数称为自由能： \[ F\left( x \right) =-\log \sum_h{\exp \left( -E\left( x,h \right) \right)} \] 一般更倾向于更为通用的基于$\log \tilde{p}_{model}\left( x \right)$的定义。

基于能量的学习为许多概率和非概率的学习方法提供了一个统一的框架，特别是图模型和其他结构化模型的非概率训练。基于能量的学习可以被看作是预测、分类或决策任务的概率估计的替代方法。由于不需要适当的归一化，基于能量的方法避免了概率模型中与估计归一化常数相关的问题。此外，由于没有标准化条件，在学习机器的设计中允许了更多的灵活性。大多数概率模型都可以看作是特殊类型的基于能量的模型，其中能量函数满足一定的归一化条件，损失函数通过学习优化，具有特定的形式。

用分类器做一个简单例子，如果输入是猫的图片，那么 E(x, label='cat')=0 ，即分类正确能量函数即为0，所以这里的能量函数其实与损失函数没有太大差别，可能是最大化数据的负对数似然。为了最小化这个能量，我们可以改变label使其适应（传统的图像分类），也可以改变来适应label。
GAN：判别器本身是一个能量函数，真实样本的能量为0。生成器尝试着生成能量更低的样本。
Self-supervised：比如我们要从当前帧预测下一帧内容，那么我们需要找到一个$E\left( x^t,x^{t+1} \right)$帧使得尽可能小即可。

受限玻尔兹曼机

受限玻尔兹曼机或者簧风琴是图模型如何用于深度学习的典型例子。 RBM~本身不是一个深层模型。相反，它有一层潜变量，可用于学习输入的表示。我们将看到RBM如何被用来构建许多的深层模型。在这里，举例展示RBM在许多深度图模型中使用的实践：它的单元被分成很大的组，这种组称作层，层之间的连接由矩阵描述，连通性相对密集。该模型被设计为能够进行高效的吉布斯采样，并且模型设计的重点在于以很高的自由度来学习潜变量，而潜变量的含义并不是设计者指定的。之后将更详细地再次讨论RBM。

标准的RBM是具有二值的可见和隐藏单元的基于能量的模型，其能量函数为： \[ E\left( v,h \right) =-b^Tv-c^Th-v^TWh \] 其中b,c和W都是无约束、实值的可学习参数。我们可以看到，模型被分成两组单元：v和h，它们之间的相互作用由矩阵W来描述。该模型在下图中以图的形式描绘。该图能够使我们更清楚地发现，该模型的一个重要方面是在任何两个可见单元之间或任何两个隐藏单元之间没有直接的相互作用（因此称为”受限”，一般的玻尔兹曼机可以具有任意连接）。

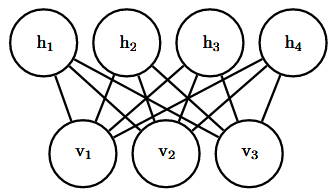
对RBM结构的限制产生了良好的属性： \[ p\left( h|v \right) =\prod_i{p\left( h_i|v \right)} \]

\[ p\left( v|h \right) =\prod_i{p\left( v_i|h \right)} \]

独立的条件分布很容易计算。对于二元的受限玻尔兹曼机，我们可以得到： \[ p\left( h_i=1|v \right) =\sigma \left( v^TW_{:,i}+b_i \right) \]

\[ p\left( h_i=0|v \right) =1-\sigma \left( v^TW_{:,i}+b_i \right) \]

结合这些属性可以得到高效的块吉布斯采样（block Gibbs Sampling)，它在同时采样所有h和同时采样所有v之间交替。

由于能量函数本身只是参数的线性函数，很容易获取能量函数的导数，例如： \[ \frac{\partial}{\partial W_{i,j}}E\left( v,h \right) =-v_ih_j \]

注：训练好的 RBM 的样本及其权重。(左) 用 MNIST 训练模型,然后用 Gibbs 采样进行采样。每一列是一个单独的 Gibbs 采样过程。每一行表示另一个 1000 步后 Gibbs 采样的输出。连续的样本之间彼此高度相关。(右) 对应的权重向量。

训练模型可以得到数据v的表示h，我们经常使用$_{h~p( h|v )}$ 作为一组描述v的特征

总的来说，RBM展示了典型的图模型深度学习方法：使用多层潜变量，并由矩阵参数化层之间的高效相互作用来完成表示学习。