Diffusion Models/Score-based Generative Models背后的深度学习原理（3）:蒙特卡洛采样法和重要采样法

2023-11-06

字数统计: 2.4k字 | 阅读时长≈ 9分

Diffusion Models/Score-based Generative Models背后的深度学习原理（3）:蒙特卡洛采样法和重要采样法

蒙特卡洛采样法

蒙特卡洛原来是一个赌场的名称，用它作为名字大概是因为蒙特卡洛方法是一种随机模拟的方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡洛方法都是为了求解一些不太好求解的求和或者积分问题。

例如下图是一个经典的用蒙特卡洛求圆周率的问题，用计算机在一个正方形之中随机的生成点，计数有多少点落在1/4圆之中，这些点的数目除以总的点数目即圆的面积，根据圆面积公式即可求得圆周率：

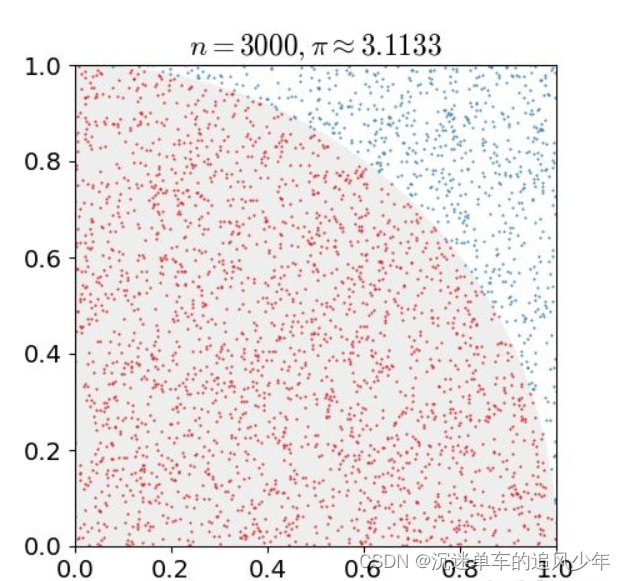
蒙特卡洛算法的另一个应用是求积分，某些函数的积分不好求，我们可以按照下面的方法将这个函数进行分解，之后转化为求期望与求均值的问题： \[ \int_a^b{h\left( x \right) dx=\int_a^b{f\left( x \right) p\left( x \right) dx=E_{p\left( x \right)}\left[ f\left( x \right) \right]}} \]

\[ E_{p\left( x \right)}\left[ f\left( x \right) \right] =\frac{1}{n}\sum{f\left( x_i \right)} \]

最终使用蒙特卡洛的方法求得积分。

对某一种概率分布p(x)进行蒙特卡洛采样的方法主要分为直接采样法、拒绝采样法与重要采样法三种：

直接采样法

直接采样的方法是根据概率分布进行采样。对一个已知概率密度函数与累积概率密度函数的概率分布，我们可以直接从累积分布函数（cdf）进行采样。

如下图所示是高斯分布的累积概率分布函数，可以看出函数的值域是(0, 1)，我们可以从U(0, 1)均匀分布中进行采样，再根据累积分布函数的反函数计算对应的x，这样就获得了符合高斯分布的N个粒子：

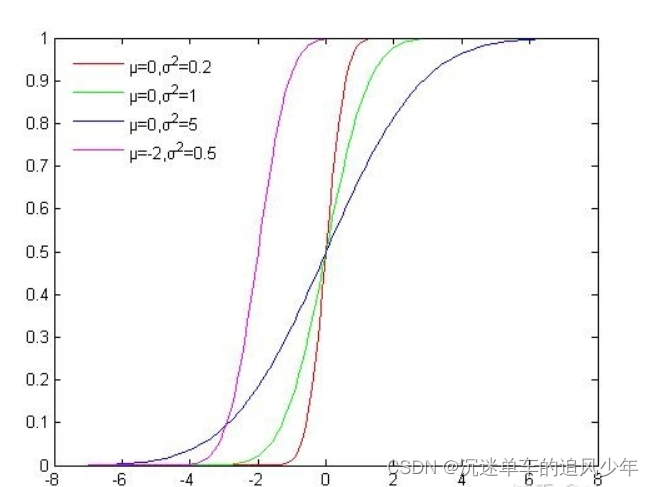
使用累积分布函数进行采样看似简单，但是由于很多分布我们并不能写出概率密度函数与累积分布函数，所以这种方法的适用范围较窄。

接受拒绝采样法

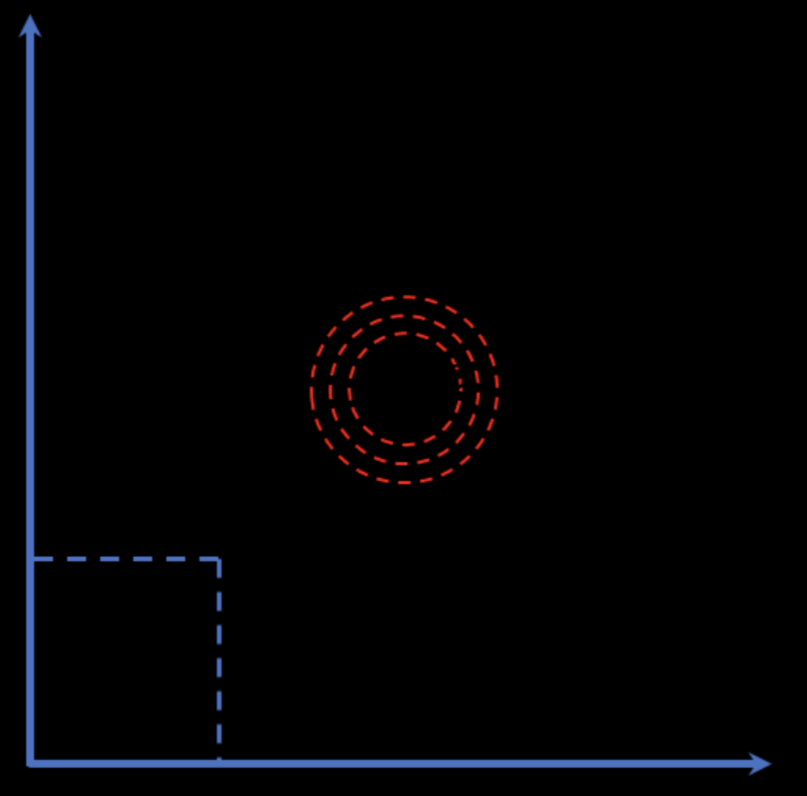
对于累积分布函数未知的分布，我们可以采用接受-拒绝采样。如下图所示，p(z)是我们希望采样的分布，q(z)是我们提议的分布(proposal distribution)，令kq(z)>p(z)，我们首先在kq(z)中按照直接采样的方法采样粒子，接下来判断这个粒子落在途中什么区域，对于落在灰色区域的粒子予以拒绝，落在红线下的粒子接受，最终得到符合p(z)的N个粒子。

采样流程如下：

1.需求：由已知分布的概率密度函数$f( x ) $，产生服从此分布的样本X

2.准备工作：

需要一个辅助的“建议分布”$G$（概率密度函数$g( y ) $ 已知）来产生候选样本。可选均匀分布、正态分布等。
还需要另一个辅助的均匀分布$U( 0,1 ) $ 。
**计算一个常数值c：满足不等式$c*g( x ) f( x ) $ 的最小值c（当然，我们非常希望c接近于1）**

3.开始样本生成：

从建议分布$G$抽样，得到样本$Y$。
从分布$U( 0,1 ) $抽样，得到样本$U$。
如果$U\le \frac{f\left( y \right)}{c*g\left( Y \right)}$，则令$X=Y$（接受$Y$),否则继续执行步骤1（拒绝）。

写一段代码吧：

import random
import math
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
 
%matplotlib inline
sns.set_style('darkgrid')
plt.rcParams['figure.figsize'] = (12, 8)
 
 
def AceeptReject(split_val):
    global c
    global power
    while True:
        x = random.uniform(0, 1)
        y = random.uniform(0, 1)
        if y*c <= math.pow(x - split_val, power):
            return x
 
power = 4
t = 0.4  
sum_ = (math.pow(1-t, power + 1) - math.pow(-t, power + 1)) / (power + 1)  #求积分
x = np.linspace(0, 1, 100)
#常数值c
c = 0.6**4/sum_
cc = [c for xi in x]
plt.plot(x, cc, '--',label='c*f(x)')
#目标概率密度函数的值f(x)
y = [math.pow(xi - t, power)/sum_ for xi in x]
plt.plot(x, y,label='f(x)')
#采样10000个点
samples = []
for  i in range(10000):
    samples.append(AceeptReject(t))
plt.hist(samples, bins=50, normed=True,label='sampling')
plt.legend()
plt.show()

重要性采样法

接受拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布(proposal distribution)的选择，如果提议分布选择的不好，可能采样时间很长却获得很少满足分布的粒子。而重要性采样就解决了这一问题。

通过采用重要抽样密度函数替换原来的抽样密度函数，使得样本落入失效域（对于求积分来说就是对积分贡献大的区域）的概率增加，以此来获得高的抽样效率和更快的收敛速度。

重要采样法是蒙特卡洛法的改进，蒙特卡洛法属于均匀抽样，大水漫灌。简单粗暴的方法后果往往就是效率低。重要采样把更多的点撒在不容易收敛的区域，怎么理解容易收敛还是难收敛呢，我通过下图说明。

我们想象一下，如果我在1区域丢两个随机采样点，那么落在积分线上和下的概率应该是差不多的，也就是一边一个的概率比较大可能是1/2，两个都落在一边的概率比较小可能是1/4。那么这样的区域不需要我丢太多点很快就收敛了。3区域就比较麻烦了，一边大一边小，那么我丢两个点，两个点都落在积分线下的概率比一边一个点的概率还要高，也就是说我丢少量点的话可能都不收敛，都没啥好效果。因此，作为蒙特卡洛的改进方法，我们的目标就是用尽量少的点，让仿真尽快收敛。那么重要采样的策略就是进行区别对待，具体问题具体分析、具体应对，将较少的点丢在容易收敛的区域，即对积分贡献小的区域、或失效概率比较大的区域、或可靠度比较低的区域。将较多的点丢在不容易收敛的区域，即对积分贡献大的区域、或失效概率较小的区域、或可靠度较大的区域。这样避免大水漫灌，无差别丢采样点，能够提高效率是直观的。

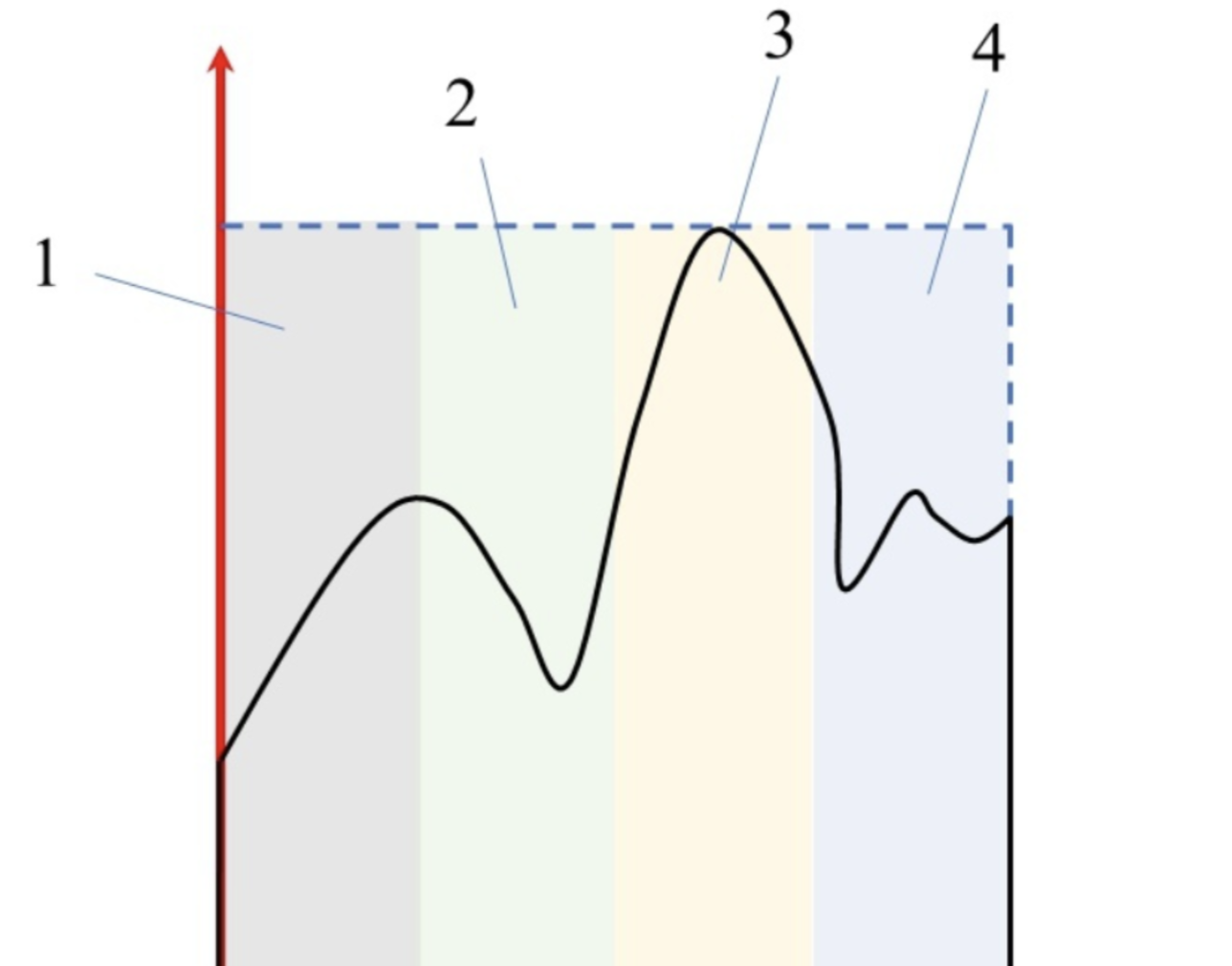
对于可靠性问题而言，如上图所示，极限状态边界以上为失效区域，边界以下为可靠区域。可考虑二维问题，假设两个响应随机变量都是高斯分布，那么如果以可靠概率密度去采样那就是黑线的等概率线的采样，我们发现，采样点多落在高斯分布的期望附近，在失效区域的点寥寥，也就是意味着这种采样方式收敛速度慢，需要抽很多点才能使得失效概率收敛。而采用重要采样，我们选取的是重要抽样密度，它的分布可以选在改进一次二阶矩方法（A-FOSM）的设计点为期望点的高斯分布，那么这时候采样点能以最快的速度分辨失效和可靠，就像我们通过移动抽样概率密度函数的中心，使得我们的抽样由上图的3区域变成1区域，以此增快收敛速度。那你可能会问了，你这样坐在极限状态边界采样岂不是概率接近1/2了？这个考虑是对的，如果只是按照蒙特卡洛方法，将采样点带入到极限状态函数，然后根据指标函数去分辨落在失效区还是可靠区，然后除以总的采样点数N，那确实是50%左右，但是重要采样不光引入了重要采样密度，还引入了权重： \[ w\left( x \right) =\frac{f_X\left( x \right)}{h_X\left( x \right)} \] 其中分子为失效概率密度，分母为重要抽样密度。那如何理解这个权重式子呢？很显然，当我们丢一个采样点x，我们就可以根据密度函数计算出分子和分母，再看上图，如果这个点x靠近黑色高斯分布的中心那就是说明分子大，权重就大；靠近红色高斯分布的中心，那就是分母大，权重就小。也就是边界点虽然多，但是权重低，那么最后在算可靠度或者失效概率时候（本质都是积分）就会得到一个被权重平衡后的计算。也可以直观的理解：离极限状态边界远的，草草几个点就能知道这块区域属于失效还是可靠，不需要浪费时间，把精力集中到边界，不容易分辨是失效还是可靠的区域，这样才能提高效率，最后再通过权重系数来把一些总和的概率为1等等条件满足即可。