Diffusion Models扩散模型与深度学习(数学原理深解)

前面的三次博客已经深入的说明了配分函数、基于能量模型、受限玻尔兹曼机、蒙特卡洛采样法和重要采样法等数学原理，这些都是扩散模型所蕴含的底层数学原理，那么现在就开始真正理解一下扩散模型。

核心问题

机器学习的一个核心问题是，使用高度灵活的概率分布族对复杂数据集进行建模，在这些概率分布族中，学习、抽样、推理和评估仍然可以通过分析或计算进行处理。

扩散模型的基本思想受到非平衡统计物理的启发，通过迭代正向扩散过程系统地、缓慢地破坏数据分布中的结构，然后学习一个反向扩散过程，恢复数据中的结构，产生了一个高度灵活和易于处理的数据生成模型。

这种方法允许我们快速学习、采样和评估数千层或时间步长的深度生成模型中的概率，以及计算学习模型下的条件概率和后验概率。

说明：扩散模型是一种很古老的模型，2020年提出的Denoising Diffusion Probabilistic Models（DDPM）去噪扩散概率取得了更好的效果，与此类似，或者在DDPM上改进的模型如：Score-Based Models、DDIM、SMLD等，原理相似。这里就以DDPM为例讲述其数学原理。

总体过程

总体过程分为正向过程和逆向过程。

扩散概率模型DDPM是一个参数化的马尔科夫链，使用变分推理来来生成有限时间 T 后与数据分配的样本。神经网络学习这条链的跃迁来逆转扩散过程，这是一条马尔科夫链，它在采样的相反方向逐渐向数据添加噪声，直到信号被破坏。

正向过程称为 q采样过程，用\(q\left( x_t|x_{t-1} \right)\)表示，这一过程可以理解为添加噪声的过程，不涉及参数分布；

逆向过程称为 p采样过程，用\(p_{\theta}\left( x_{t-1}|x_t \right)\)表示，这一过程是从噪声中重建出数据分布的过程。

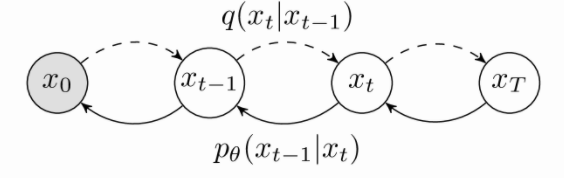
前向过程（Diffusion Process）

要从给定一个从真实数据分布 X0 ~ q（x）中抽样的数据点，前向过程在 0~T 时间步长内逐步添加噪声，产生一系列有噪声的样本：\(x_1,...,x_T\)

扩散模型与其他类型的潜在变量模型的区别在于近似后验\(q\left( x_{1:T}|x_0 \right)\)是一个固定的马尔科夫链，因此可以写成： \[ q\left( x_{1:T}|x_0 \right) :=\prod_{t=1}^T{q\left( x_t|x_{t-1} \right)} \] 添加高斯噪声的数据通过variance schedule \(\beta _1,...,\beta _T\)控制，由于前向过程是固定的马尔科夫链，因此variance schedule \(\beta _t\)也是固定的，实际代码中可以通过一个固定的variance schedule表来获取。从全局考虑，越接近数据分布添加的噪声对数据分布的影响越大，反之越小。所以后来人用 cos 函数、指数函数 等方法获取\(\beta _t\)，取得了更好的效果。但是需要保证\(\beta _t\)足够小这一假设，因为只有\(\beta _t\)足够小，逆向过程的\(p_{\theta}\left( x_{t-1}|x_t \right)\)才是符合高斯分布的，这是我们推导的一个重要前提。

因此\(q\left( x_t|x_{t-1} \right)\)可以定义为： \[ q\left( x_t|x_{t-1} \right) :=N\left( x_t;\sqrt{1-\beta _t}x_{t-1},\beta _tI \right) \] 推导过程如下：

推导过程中使用VAE中提出的reparameterization trick，为了方便表示q采样累成过程，定义：

• \(\alpha _t=1-\beta _t\)
• \(\bar{\alpha}_t=\prod_{i=1}^T{\alpha _i}\)

可得 \(x_t\)：

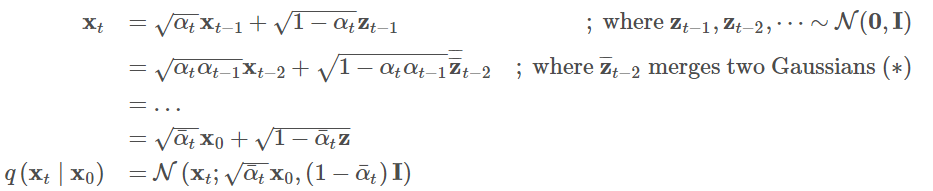
reparameterization trick是VAE中的知识点：损失函数中的期望项从z ~ \(q_{\phi}\left( z|x \right)\)中生成样本，抽样是一个随机过程，因此我们不能反向传播梯度。为了使其可训练，引入了reparameterization trick重参数化技巧：通常可以将随机变量z表示为确定性变量\(z=T_{\phi}\left( x,\epsilon \right)\)，其中\(\epsilon\)是辅助独立随机变量，变换函数\(T_{\phi}\)通过\(\phi\)参数化将\(\epsilon\)转换为\(z\)。

例如：

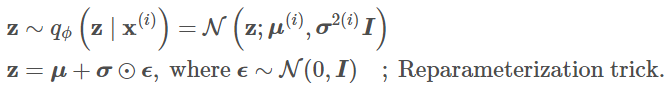
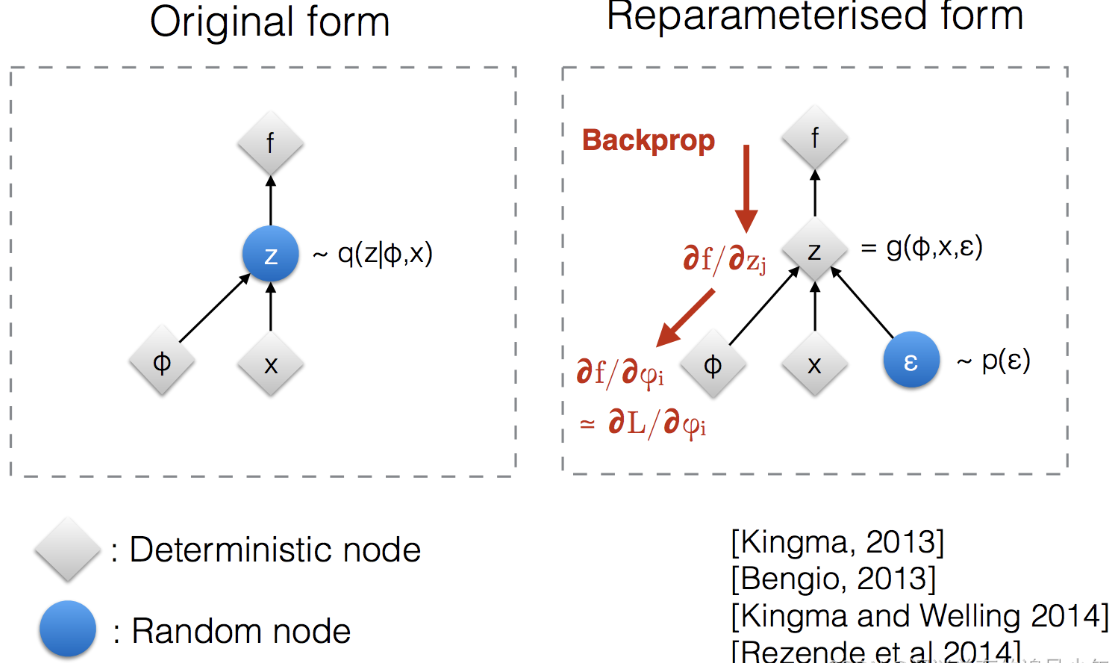
注：图例说明重参数化技巧如何使抽样过程可训练

这里再详细补充一些吧。

Reparameterization trick（重参数化技巧）是一种在训练生成模型中处理随机性潜在变量的方法，特别常见于变分自动编码器（VAE）等模型中。这个技巧的目的是使模型可微分（differentiable），以便使用梯度下降等反向传播算法来训练模型，也就是将随机采样的过程转换为可导的运算，从而使得梯度下降算法可以正常工作。

以下是它的基本原理和操作：

• 1.背景：在生成模型中，通常会有一个随机性的潜在变量，例如高斯分布中的均值和方差，用于生成样本。这会导致问题，因为采样操作是不可微的，无法通过反向传播来更新梯度，从而让模型学习这些分布参数。
• 2.重参数化：为了解决这个问题，Reparameterization trick 提出将随机采样操作从网络中移动到一个确定性函数中。这个确定性函数通常是一个线性变换，将从标准高斯分布（均值为0，方差为1）中采样的随机噪声与潜在变量的均值和标准差相结合。这个确定性函数是可微分的，因此梯度可以在这个过程中传播。
• 3.具体操作：在实际操作中，首先从标准高斯分布中采样一个随机噪声向量（通常记作𝝐）。然后，通过一个神经网络或其他可微分的映射函数，将这个随机噪声向量与模型的均值和标准差参数相结合，生成最终的潜在变量。这个潜在变量被用于生成样本，同时也与损失函数相关联，使得可以通过反向传播来更新梯度。

举个栗子：

Variational Bipartite Graph Encoder中作者有这样一个操作：

上面(3)式子，和VAE的讲解结合起来看看，貌似能理解了。首先 Z 服从 N(μ,σ2)的话，大学概率论都学过，那么\(ε = σ \frac{(Z-μ)}{σ}\)就服从标准正态分布了，也就是 ε 服从标准正态分布N(0, 1)。 \(ε = σ \frac{(Z-μ)}{σ}\)左边的等式变式一下，就有Z = μ + ε × σ了，那么从 N(μ,σ2)采样一个Z，相当于从从标准正态分布N(0, 1)采样一个 ε 。这样就将随机采样的过程转换为可导的运算，可以进行反向传播了。

总之，“Reparameterization trick” 允许模型在训练过程中通过随机采样得到的潜在变量，同时保持了可微性，从而使生成模型更容易优化。这个技巧在生成对抗网络（GANs）、变分自动编码器（VAE）和其他生成模型中广泛应用。

采样过程（Reverse Diffusion Process）

如果我们能逆转上述前向过程，从\(q\left( x_{t-1}|x_t \right)\)当中采样，我们就能从\(x_T\)得到\(x_0\)。我们前面说明\(\beta _t\)足够小假设的时候说明了\(q\left( x_{t-1}|x_t \right)\)也是符合高斯分布的。但是我们很难得到整个数据集的\(q\left( x_{t-1}|x_t \right)\)概率分布，因此我们需要学习一个模型\(p_{\theta}\)来近似这些条件概率以便进行反向扩散过程： \[ p_{\theta}\left( x_0:T \right) =p\left( x_T \right) \prod_{t=1}^T{p_{\theta}\left( x_{t-1}|x_t \right) \ \ p_{\theta}\left( x_{t-1}|x_t \right) =N\left( x_{t-1};\mu _{\theta}\left( x_t,t \right) ,\sum_{\theta}{\left( x_t,t \right)} \right)} \] 我们还是手写一遍推导过程：

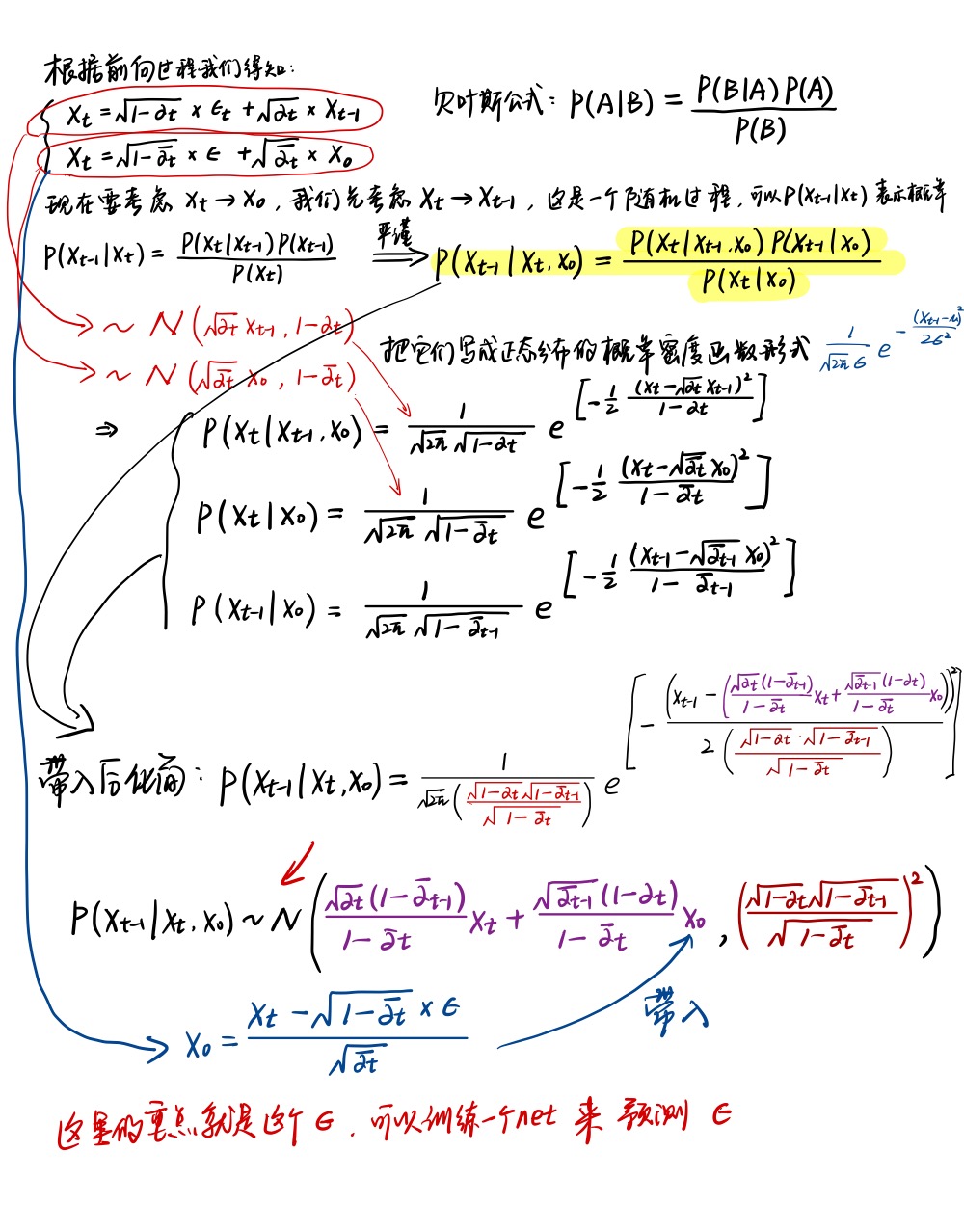
其中反向过程的示意图可以这样画：

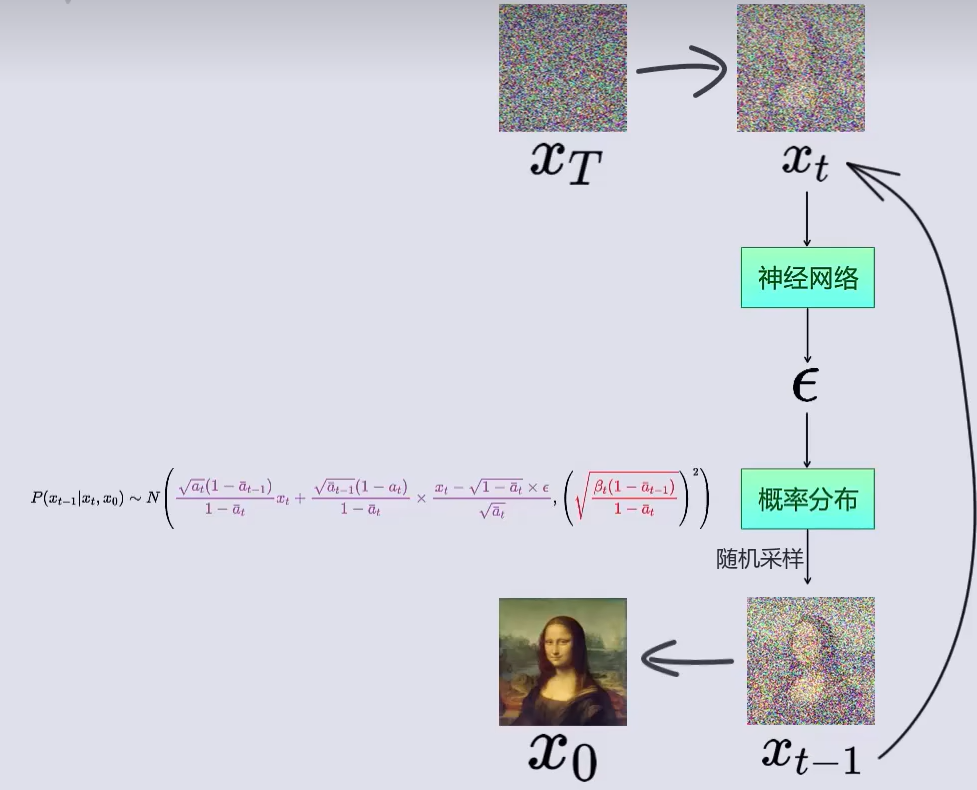
为了简化后面的推导，我们可以这样写： \[ p\left( x_{t-1}|x_t,x_0 \right) \ ~\ N\left( x_{t-1};\tilde{\mu}_t\left( x_t,x_0 \right) ,\tilde{\beta}_tI \right) \] \[ where\ \tilde{\mu}_t\left( x_t,x_0 \right) =\frac{\sqrt{\alpha _t\left( 1-\bar{\alpha}_{t-1} \right)}}{1-\bar{\alpha}_t}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}\beta _t}{1-\bar{\alpha}_t}\frac{1}{\sqrt{\bar{\alpha}_t}}\left( x_t-\sqrt{1-\bar{\alpha}_t}z\epsilon \right) \] \[ =\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) \] \[ and\ \ \ \bar{\beta}_t:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta _t \]

推导训练目标

引入变分分布 q 后可以写出关于似然函数\(p_{\theta}\)的变分界限： \[ -\log p_{\theta}\left( x_0 \right) \le -\log p_{\theta}\left( x_0 \right) \ +\ D_{KL}\left( q\left( x_{1:T}|x_0 \right) ||p_{\theta}\left( x_{1:T}|x_0 \right) \right) \] \[ =-\log p_{\theta}\left( x_0 \right) +\mathbb{E}_{x_1:T~q\left( x_1:T|x_0 \right)}\left[ \log \frac{q\left( x_{1:T}|x_0 \right)}{p_{\theta}\left( x_{0:T} \right) /p_{\theta}\left( x_0 \right)} \right] \] \[ =-\log p_{\theta}\left( x_0 \right) +\mathbb{E}_q\left[ \log \frac{q\left( x_{1:T}|x_0 \right)}{p_{\theta}\left( x_{0:T} \right)}+\log p_{\theta}\left( x_0 \right) \right] \] \[ =\mathbb{E}_q\left[ \log \frac{q\left( x_{1:T}|x_0 \right)}{p_{\theta}\left( x_{0:T} \right)} \right] \] 所以： \[ L_{VLB}=\mathbb{E}_{q\left( x_{0TT} \right)}\left[ \log \frac{q\left( x_{1:T}|x_0 \right)}{p_{\theta}\left( x_{0:T} \right)} \right] \ge -\mathbb{E}_{q\left( x_0 \right)}\log p_{\theta}\left( x_0 \right) \] 这里有些部分可能看不懂，做一些额外的解释：

• \(D_{KL}\)这里指的是KL散度，这是一个用来衡量两个概率分布的相似性的一个度量指标。
• 信息熵为：\(H=-\sum_{i=1}^N{p\left( x_i \right) \log p\left( x_i \right)}\)
• 在信息熵的基础上，我们定义 KL 散度为：\(D_{KL}\left( p||q \right) =\sum_{i=1}^N{p\left( x_i \right) \cdot \left( \log \frac{p\left( x_i \right)}{q\left( x_i \right)} \right)}\)
• \(D_{KL}\left( p||q \right)\)表示的就是概率 q 与概率 p 之间的差异，很显然，散度越小，说明 概率 q 与概率 p 之间越接近，那么估计的概率分布于真实的概率分布也就越接近。

使用Jenson不等式也可以直接得到相同的结果，假设我们想要最小化交叉熵最为学习目标：

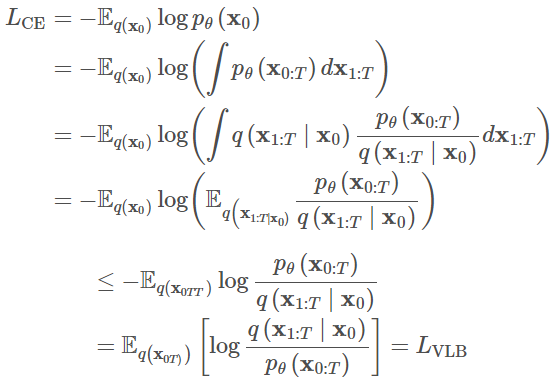
为了将方程中的每一项转化为可解析计算，目标可以进一步改写为几个KL散度和熵项的组合，通过随机梯度下降优化L的随机项：

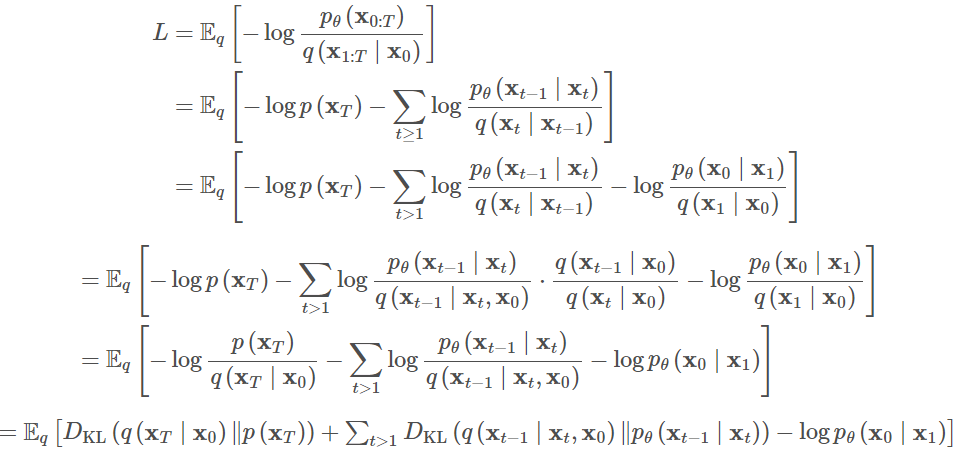
所以随机梯度下降的目标为：

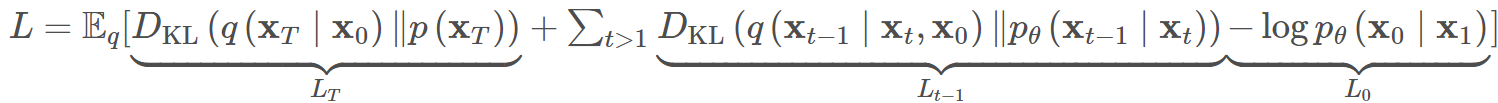
因为XT，X0，X1的分布都是确定的，所以LT、L0都是常数，求导后可以省略，所以L可再简化为只含有Lt-1的想，为了表达方便我们写成Lt： \[ L_t=\mathbb{E}_{x_0,z}\left[ \frac{1}{2||\sum_{\theta}{\left( x_t,t \right) ||\begin{array}{c} 2\\ 2\\ \end{array}}}||\tilde{\mu}_t\left( x_t,x_0 \right) -\mu _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{1}{2||\sum_{\theta}{||\begin{array}{c} 2\\ 2\\ \end{array}}}||\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) -\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right) \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{\beta _{t}^{2}}{2\alpha _t\left( 1-\bar{\alpha}_t \right) ||\sum_{\theta}{\,\,||\begin{array}{c} 2\\ 2\\ \end{array}}}||\epsilon -\epsilon _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \text{}\\ \end{array} \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{\beta _{t}^{2}}{2\alpha _t\left( 1-\bar{\alpha}_t \right) ||\sum_{\theta}{\,\,||\begin{array}{c} 2\\ 2\\ \end{array}}}||\epsilon _t-\epsilon _{\theta}\left( \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon ,t \right) ||\begin{array}{c} 2\\ \\ \text{}\\ \end{array} \right] \] \[ L_t=\mathbb{E}_{x_0,z}\left[ \frac{1}{2||\sum_{\theta}{\left( x_t,t \right) ||\begin{array}{c} 2\\ 2\\ \end{array}}}||\tilde{\mu}_t\left( x_t,x_0 \right) -\mu _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{1}{2||\sum_{\theta}{||\begin{array}{c} 2\\ 2\\ \end{array}}}||\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) -\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right) \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{\beta _{t}^{2}}{2\alpha _t\left( 1-\bar{\alpha}_t \right) ||\sum_{\theta}{\,\,||\begin{array}{c} 2\\ 2\\ \end{array}}}||\epsilon -\epsilon _{\theta}\left( x_t,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right] \] \[ =\mathbb{E}_{x_0,z}\left[ \frac{\beta _{t}^{2}}{2\alpha _t\left( 1-\bar{\alpha}_t \right) ||\sum_{\theta}{\,\,||\begin{array}{c} 2\\ 2\\ \end{array}}}||\epsilon _t-\epsilon _{\theta}\left( \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon ,t \right) ||\begin{array}{c} 2\\ \\ \\ \end{array} \right] \]

训练扩散模型时，忽略加权项的简化目标效果更好： \[ L_{t}^{simple}=\mathbb{E}_{x_{0,z_t}}\left[ ||\epsilon -\epsilon _{\theta}\left( \sqrt{\bar{\alpha}_{\theta}x_0}+\sqrt{1-\bar{\alpha}_t}\epsilon ,t \right) ||\begin{array}{c} 2\\ \\ \text{ }\\ \end{array} \right] \] 其中\(z_\theta\)可以理解为使用神经网络对噪声预测，此处的噪声可以看成是数据分布的增广，此处的神经网络一般用Unet，至于为什么要用Unet，我会再写一篇博客。

至此，我们正式推出了完整训练目标，也就得到了原论文中的训练伪代码：