为什么Diffusion Models扩散模型可以成为Score-based Models

之前已经对DDPM有过十分详细的推导和理解：

Diffusion Models深解

正向过程与反向过程

下图表示了全过程，其中\(x_0\)是完整的原先分布，，所以位于上方的p过程是从噪声反向重建，位于下方的q过程是从完整分布训练过程。

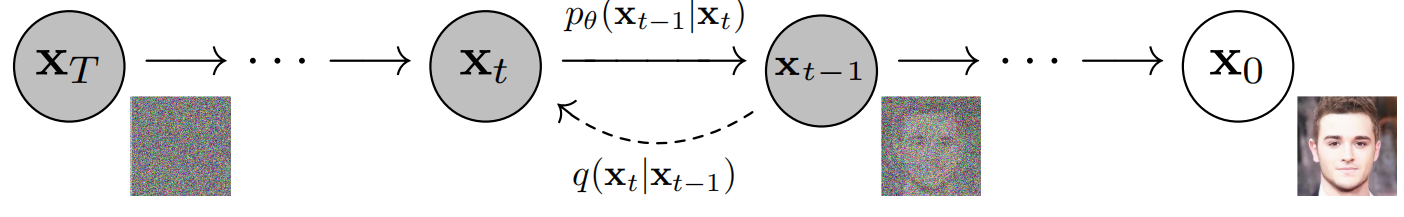
用公式表示则为：

反向过程：

\[ p_{\theta}\left( x_0:T \right) =p\left( x_T \right) \prod_{t=1}^T{p_{\theta}\left( x_{t-1}|x_t \right)} \]

\[ p_{\theta}\left( x_{t-1}|x_t \right) =N\left( x_{t-1};\mu _{\theta}\left( x_t,t \right) ,\sum_{\theta}{\left( x_t,t \right)} \right) \]

正向过程：

\[ q\left( x_{1:T}|x_0 \right) :=\prod_{t=1}^T{q\left( x_t|x_{t-1} \right)} \]

\[ q\left( x_t|x_{t-1} \right) :=N\left( x_t;\sqrt{1-\beta _t}x_{t-1},\beta _tI \right) \]

参数解释：

\(\beta _1,\beta _2......\beta _t\)：前向过程方差。在训练中一般固定，与t的值一一对应。

\(\alpha _1,\alpha _2......\alpha _t\)：\(\alpha _t=1-\beta _t\) 。与\(\beta _t\) 一样，一般固定。

训练目标

训练目标用对数似然估计表示：

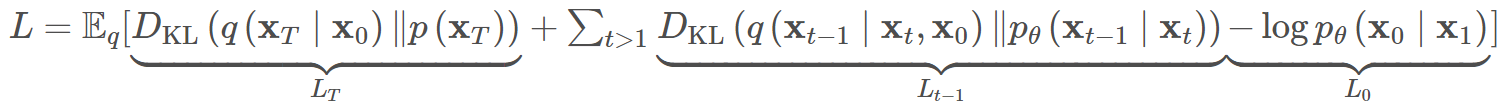
刚才说了\(\beta,\alpha\)一般是固定值，因此利用随机梯度下降法可以化简上面的似然对数训练目标：

因为\(x_t\)代表最终时刻，也就是全为噪声的时刻，所以\(L_T\)是常数，\(L_0\)可以忽略，因此训练目标就可以化简成只含有剩下的这一项：

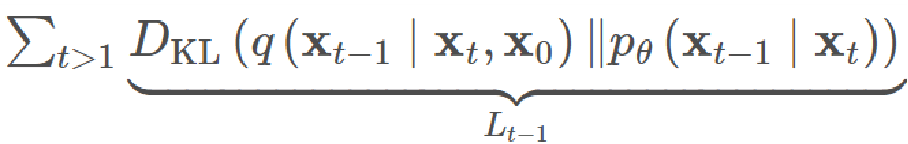
化简训练目标

我们已经把训练目标化简了，但是这还不够，接下来进一步化简。

因为： \[ p_{\theta}\left( x_{t-1}|x_t \right) =N\left( x_{t-1};\mu _{\theta}\left( x_t,t \right) ,\sum_{\theta}{\left( x_t,t \right)} \right) \] 又因为：(因为只考虑对角线) \[ \sum_{\theta}{\left( x_t,t \right)}=\sigma _{t}^{2}I \] 代表未经训练的时间相关常数，所以进一步化简为： \[ p_{\theta}\left( x_{t-1}|x_t \right) =N\left( x_{t-1};\mu _{\theta}\left( x_t,t \right) ,\sigma _{t}^{2}I \right) \] 将协方差带入后，我们的训练目标就变成了这样： \[ L_{t-1}=\mathbb{E}_q\left[ \frac{1}{2\sigma _{t}^{2}}||\tilde{\mu}_t\left( x_t,x_0 \right) -\mu _{\theta}\left( x_t,t \right) ||_{}^{2} \right] +C \]

从训练目标解释为什么又称为score-based models

从我们刚才推导出来的训练目标来看，我们最终的训练目标化简成两个均值之间的距离，再除以一个常数。

其中\(\tilde{\mu}_t\left( x_t,x_0 \right)\)代表从\(x_0\)逐渐添加噪声得到\(x_t\)的均值，\(\mu _{\theta}\left( x_t,t \right)\)代表神经网络重建匹配得到的均值。

要让这两个score匹配，因为匹配了才能使训练目标最小化，所以Diffusion Model又称为 score-based model。

从数据的匹配到噪声的匹配

不管是GAN还是VAE，都是从数据重建数据，但是通过上面的推导，DDPM实现了从通过神经网络预测含有重建信息的噪声，达到重建的效果。

实际上，噪声可以看成数据的增广，代表更广泛的数据分布。而t时刻包含了原本数据分布信息。

这个特点为后来用潜在变量\(z\)约束噪声生成、二分法查找\(z\)降低训练难度等优化方法提供了可能性。

噪声重建相比于数据重建有什么好处呢？

VAE和GAN都需要对抗训练，带来模型坍缩的问题，这个问题在Diffusion Model上可以解决。