DiffuseVAE:完美结合VAE 和 Diffusion Models

VAE 简介

在Diffusion Models面前，VAE是一个古老而经典的生成式模型，先简单介绍一下。

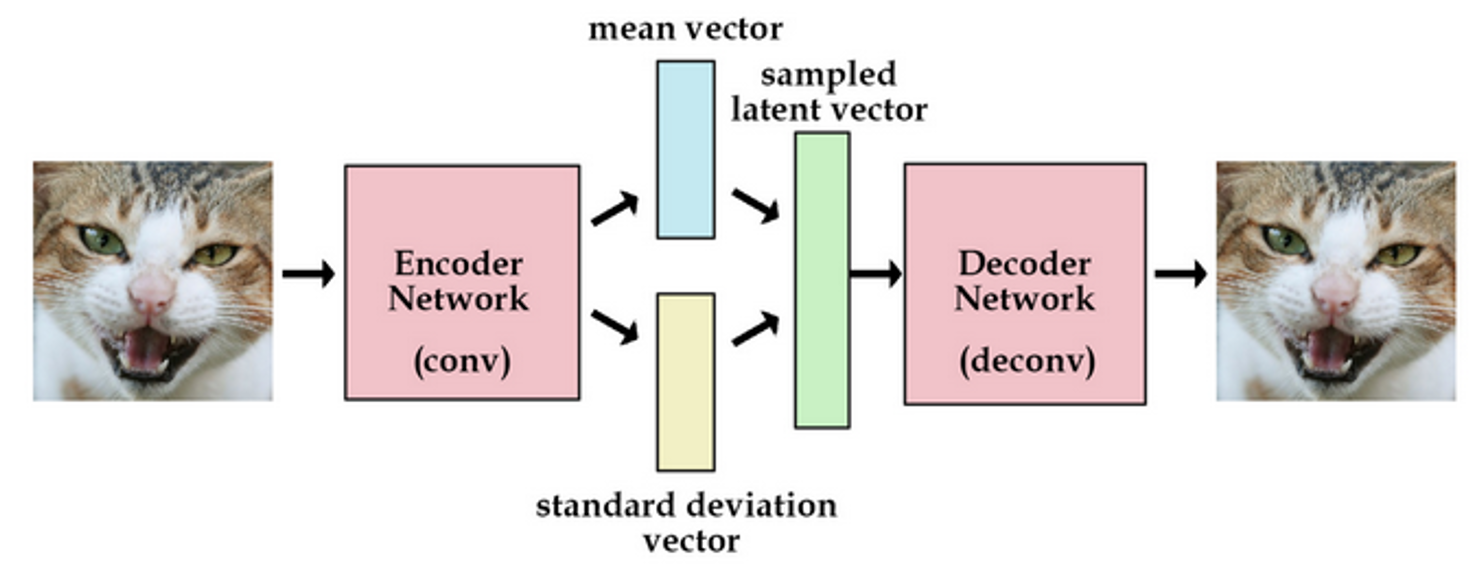
变分自动编码机从自动编码机演化而来，整个训练框架就是在对样本x进行编解码。

\(q\) 是将样本 \(x\) 编码为隐变量 \(z\)，而 \(p\) 又将隐含变量 \(z\) 解码成\(f(z)\)，进而最小化重构误差。

训练的目的是学习出编码器的映射函数和解码器的映射函数，所以训练过程实际上是在进行变分推断，即寻找出某一个函数来优化目标。因此取名为变分编码器VAE(Variational Auto-encoder)。

由于解码器无法梯度反转，所以VAE提出了重参数化的trick，这个trick在DDPM推导中同样使用了。

VAE的训练目标是最大化数据对数似然的证据下限（ELBO）： \[ \mathcal{L}\left( \theta ,\phi \right) =\mathbb{E}_{q_{\phi}\left( z|x \right)}\left[ \log p_{\theta}\left( x|z \right) \right] -\mathcal{D}_{KL}\left[ q_{\phi}\left( z|x \right) ||p\left( z \right) \right] \]

VAE优缺点与DDPM优缺点

VAE优缺点

VAE基于显式似然的生成模型，通常也用于学习数据的低维潜在表示。

一个显著的劣势就是没有对抗网络，不能融合高频信息，所以会更趋向于产生模糊的图片。

先进的生成式模型都需要更大维度的潜在空间，因此VAE生成样本质量，与隐式似然相对应的GANs相比存在显著的差距。

DDPM优缺点

去噪扩散概率模型(DDPM)需要昂贵的迭代采样过程，并且缺乏低维的潜在表示，限制了这些模型对下游应用的实际适用性。

DDPM + VAE：完美结合二者优点

论文：DiffuseVAE: Efficient, Controllable and High-Fidelity Generation from Low-Dimensional Latents

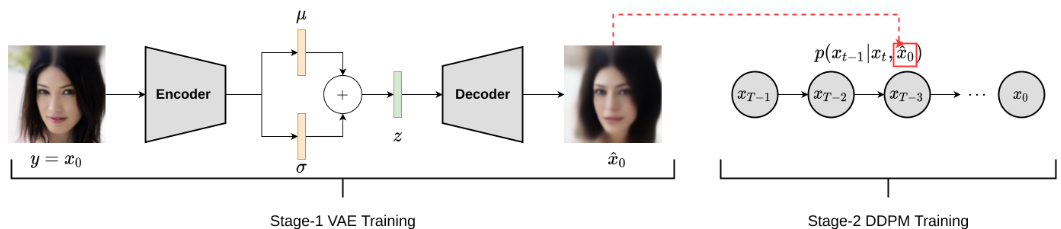
生成过程拆解成VAE和DDPM两个阶段。在第一阶段，任何任意条件作用信号 \(y\) 都可以首先使用单个随机层VAE建模。在第二阶段，使用以 \(y\) 为条件的DDPM和 \(y\) 的低维VAE潜码表示对训练数据 \(x\) 进行建模。即第一阶段对训练数据拟合成VAE，第二阶段使用以训练数据的VAE重建( \(\hat{x}\) ) 为条件的DDPM对 \(x\)进行建模。

在之前条件DDPM中的内容聊过，后续很多文章的创新点都放在怎样加入condition约束生成上。这篇VAE结合DDPM的方法同样属于条件DDPM的范畴。

现在加入VAE信息变成了一种低维空间上的约束，而t-1时刻的数据可以看成一种高维数据方面的约束。有了低维空间+高维空间两种约束，更加强大的condition作用下，能够重建出更合理的数据分布。

有监督生成？无监督生成？

在条件DDPM的博客中就聊过，引入latent \(z\)，甚至直接引入原图基础上相关的某种flow，本质上将个无监督学习变成了有监督学习。所以作者要证明这个结构的优越性/有效性，必须要证明在unconditional 上的表现，这也是所有condition方面做创新的DDPM论文必须要说明清楚的一点。

与GANs的训练类似，生成器和鉴别器训练最好不是同步的，同时也为了证明unconditional情景下的生成能力，需要先在没有条件的输入下训练DDPM，即关注 \(p_{\phi}\left( x_{0:T}|z \right)\) 分布，然后用两阶段优化的方式，先优化VAE，再优化DDPM。

引用：

• https://arxiv.org/abs/2201.00308
• https://github.com/kpandey008/DiffuseVAE
• https://www.cnblogs.com/huangshiyu13/p/6209016.html
• https://xduwq.blog.csdn.net/article/details/120861817
• https://xduwq.blog.csdn.net/article/details/122802646