从VAE到Diffusion Models

Diffusion Model简史

GANs诞生于2014年，diffusion model比GANs小一岁，第一篇difusion model论文《DeepUnsupervised Learning using Nonequilibrium Thermodynamics》发表与2015年。这两种全新的生成式模型刚被提出来的时候，都是一个全新的理论，但在各种任务运用上效果并不是非常理想。只不过GANs诞生后，DCGAN、WGAN等GANS的变式模型在各种任务上取得了巨大的成功，很快GANs便变得非常流行。

diffusion model沉寂了好几年，直到2020年《Denoising Diffusion Probabilistic Models》以稳定的变分目标训练的模型在图像生成方面可以匹配或超过GANs。随后在论文《Score-Based GenerativeModeling through Stochastic Differential Equations》论文中，diffusion model被证明与基于分数的模型score-based model有着密切的联系，这两种模型最近在随机微分方程的框架下得到统一。 时间来到2021年，diffusion model的论文如雨后春笋一般冒出，在图片生成、语音生成、视频生成、文本生成、三维模型生成、时间序列生成、点云生成等方面取得了巨大成功。

温习VAE

我们考虑以下的生成模型： \[ p_{\theta}\left( x \right) =\int_z{p_{\theta}\left( x|z \right) p_{\theta}\left( z \right)} \] 其中 \(z\) 代表潜在的数据分布，\(x\) 代表真实的数据分布。我们用MLE估计模型参数，用蒙特卡洛采样近似 \(z\) 上的积分，方程如下： \[ \theta ^*=\underset{\theta}{arg\max}\mathbb{E}_{x~\hat{p}\left( x \right) ,z~p\left( z \right)}\left[ \log\text{\ }p_{\theta}\left( x|z;\theta \right) \right] \] 但是这种方法不缩放到高维的 \(z\) ，因为一个随机的潜在编码 \(z\) 的可能性 \(p(z)\) 对应于任何特定高维中的数据点都是非常小的。

所以VAE通过从一个新的分布\(q_{\phi}\left( z|x \right)\)当中进行采样，并与生成模型一起优化，将其写为： \[ \log\text{\ }p\left( x \right) \ge \mathbb{E}_{z~q_{\phi}\left( z|x \right)}\left[ \log\text{\ }\frac{p_{\theta}\left( x|z \right) p\left( z \right)}{q_{\phi}\left( z|x \right)} \right] \] 神经网络训练过程中肯定需要求解梯度，VAE中有一个著名的重参数化技巧，将采样过程定义为确定性的数据依赖函数和数据独立噪声的组合，避免了直接求解梯度。

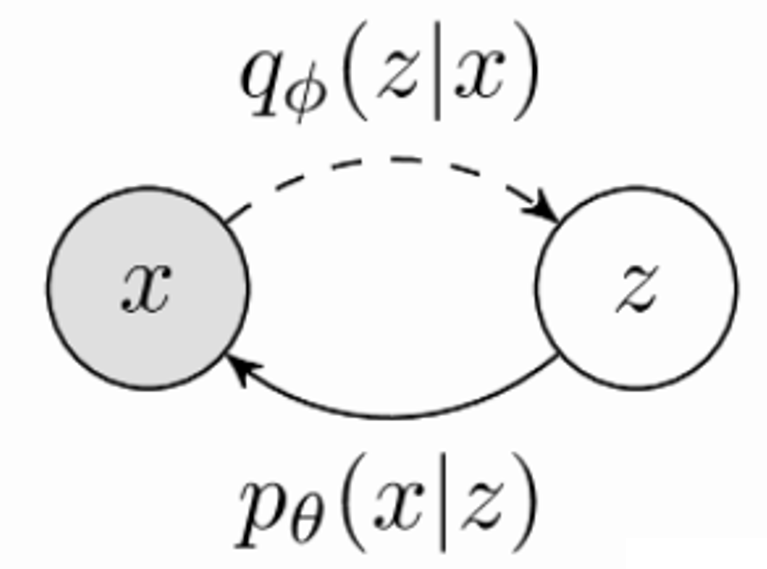
从VAE到层次VAE

我们这里引入了两个潜在变量 \(z_1\) 和 \(z_2\)，我们的联合分布便写成了： \[ p\left( x \right) =\int_{z1}{\int_{z2}{p_{\theta}\left( x,z_1,z_2 \right) dz_1,dz_2}} \] 同样的，我们的优化目标模型转移图就成了： \[ \log\text{\,\,}p\left( x \right) \ge \mathbb{E}_{z1,z2~q_{\phi}\left( z1,z2|x \right)}\left[ \log\text{\,\,}\frac{p_{\theta}\left( x,z_1,z_2 \right)}{q_{\phi}\left( z_1,z_2|x \right)} \right] \]

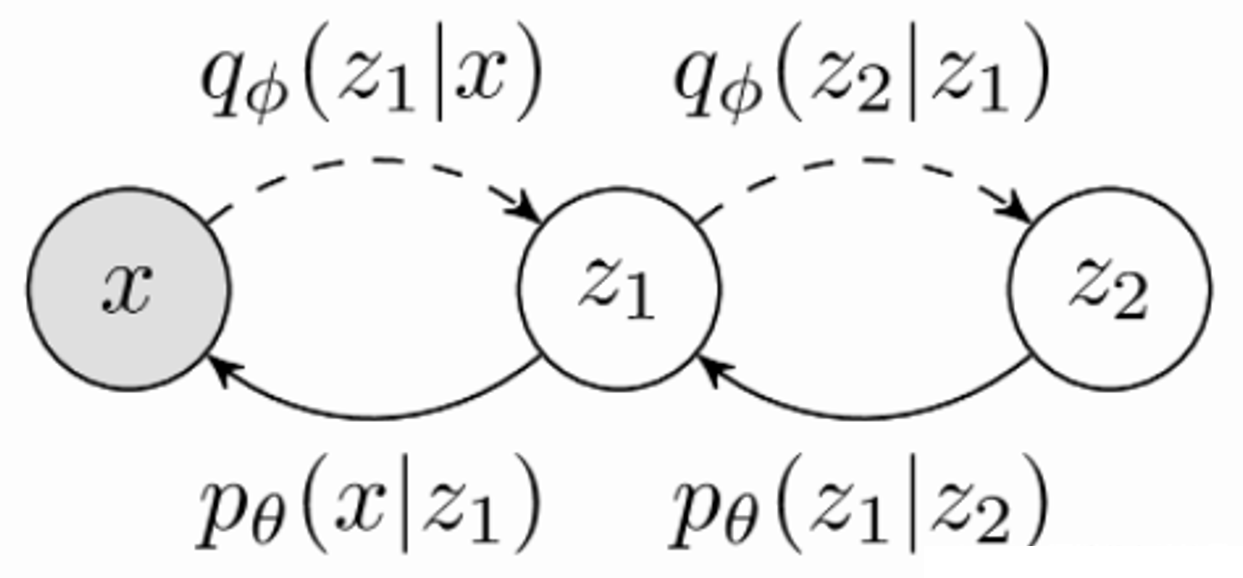
从层次VAE到Diffusion Probabilistic Models

我们考虑在一个 0-T 的时间内，逐渐往原始数据中添加噪声，添加的噪声逐渐增加：

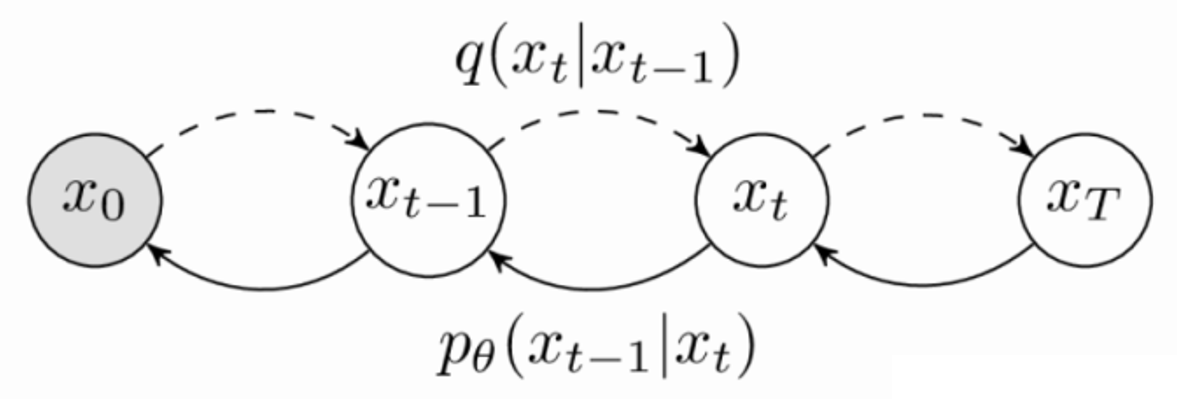
我们将Diffusion Model看成多个分层的VAE来实现，将它们区别开来的是一个独特的推理模型，它不包含可学习的参数，并且被构造成最终的潜在分布 \(q(x_T)\)，收敛于一个标准高斯分布。

Diffusion Model的变分下界写成： \[ -\mathcal{L}=\mathbb{E}_q\left[ -\log p\left( x_T \right) -\sum_{t\ge 1}^T{\log \frac{p_{\theta}\left( x_{t-1}|x_t \right)}{q\left( x_t|x_{t-1} \right)}} \right] \]

注意将其对比层次VAE的变分下界看。

我们不需要再训练的每一步上做一个完整的正向和反向过程，只需要在每一个minibatch中优化\(p_{\theta}\left( x_{t-1}|x_t \right)\)即可。

从Diffusion Probabilistic Models到Denoising Diffusion Probabilistic Mdoels

首先假设数据符合高斯分布，并且数据分布之间是独立的（独立性假设），关于这一部分的推导可以看之前的博客。 \[ p\left( x_{t-1}|x_t,x_0 \right) \ ~\ N\left( x_{t-1};\tilde{\mu}_t\left( x_t,x_0 \right) ,\tilde{\beta}_tI \right) \]

\[ where\ \tilde{\mu}_t\left( x_t,x_0 \right) =\frac{\sqrt{\alpha _t\left( 1-\bar{\alpha}_{t-1} \right)}}{1-\bar{\alpha}_t}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}\beta _t}{1-\bar{\alpha}_t}\frac{1}{\sqrt{\bar{\alpha}_t}}\left( x_t-\sqrt{1-\bar{\alpha}_t}z\epsilon \right) \]

\[ =\frac{1}{\sqrt{\alpha _t}}\left( x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) \]

\[ and\ \ \ \bar{\beta}_t:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta _t \]

记为方程(1)

用\(x_0\)表示原始的数据分布，\(x_t\)表示t时刻的数据分布。根据上面的推导，用\(x_t\)表示\(x_0\)： \[ x_t\left( x_0,\epsilon \right) =\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon \] 同样的，\(x_0\)可以用\(x_t\)表示为： \[ x_0=\frac{x_t\left( x_0,\epsilon \right) -\sqrt{1-\bar{\alpha}_t}\epsilon}{\sqrt{\bar{\alpha}_t}} \] 我们的优化目标可以写成： \[ L_{t-1}=\mathbb{E}_{t,xt,x0}\left[ \frac{1}{2\sigma _{t}^{2}}||\tilde{\mu}_t\left( x_t,x_0 \right) -\mu _{\theta}\left( x_t,t \right) || \right] +C \] 前向过程的后验分布写成\(x_t\left( x_0,\epsilon \right)\)，方程(1)就可以化简成： \[ \tilde{\mu}_t\left( x_t\left( x_0,\epsilon \right) ,\frac{1}{\sqrt{\bar{\alpha}_t}}\left( x_t\left( x_0,\epsilon \right) -\sqrt{1-\bar{\alpha}_t}\epsilon \right) \right) \] \[ =\frac{\beta _t\sqrt{\bar{\alpha}_{t-1}}\left( x_t-\epsilon \sqrt{1-\bar{\alpha}_t} \right)}{\sqrt{\bar{\alpha}_t}\left( 1-\bar{\alpha}_t \right)}+\frac{\sqrt{\alpha _t}\left( 1-\bar{\alpha}_{t-1} \right)}{1-\bar{\alpha}_t}x_t \] \[ =\left( \frac{\beta _t\sqrt{\bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_t}\left( 1-\bar{\alpha}_t \right)}+\frac{\sqrt{\alpha _t}\left( 1-\bar{\alpha}_{t-1} \right)}{1-\bar{\alpha}_t} \right) x_t-\frac{\beta _t\sqrt{\bar{\alpha}_{t-1}}\sqrt{1-\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}\left( 1-\bar{\alpha}_t \right)} \]

至此，我们的训练目标进一步化简： \[ L_{t-1}-C=\mathbb{E}_{x0,\epsilon ,t}\left[ \frac{1}{2\sigma _{t}^{2}}\lVert \frac{1}{\sqrt{\alpha _t}}.\left( x_t\left( x_0,\epsilon \right) -\frac{\beta _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) -\mu _{\theta}\left( x_t\left( x_0,\epsilon \right) ,t \right) ||\right] \] 经过上述的推导，我们已经从最开始的预测数据分布变为：提供模型预测仿射变换。这个仿射变换是一个与时间相关的常数和一个自由参数的组合。这种参数化方法，只需要用神经网络负责预测噪声的柱状结构。至此我们从学习数据分布变成学习噪声分布，噪声可以看成数据分布的增广，蕴含了许多潜在的数据分布信息。

所以省略掉前置diffusion固定参数，最终的化简目标就可以写成： \[ \mathbb{E}_{x0,\epsilon ,t}\left[ \lVert \epsilon -\epsilon _{\theta}\left( x_t\left( x_0,\epsilon \right) ,t \right) || \right] \]

总结：VAE和Diffusion Model的异同

相同之处：

• 在逆向过程中，将一些潜在变量进行采样，并用神经网络将其转化为数据.
• 有相应的正向过程，将数据转化为一系列的潜在表征.
• 训练目标是数据似然的下界，可以用类似于VAE的方式导出.
• DDPM中使用的变分边界强调了与变分自动编码器和神经压缩的进一步联系

不同之处：

• DDPM中的正向过程没有学习参数
• DDPM中的正向过程逐步破坏所有关于输入的信息，这样最终的分布q(xT|x0)通过构造是一个标准高斯分布。但是对于VAEs，却希望z包含关于x的一些信息。
• 在DDPM中，每个潜在值的维数必须与数据匹配。在VAEs中，可以降低维度.
• 在DDPM中，每个生成层共享相同的神经网络参数。（因为网络较深，并且存在大量重复信息，设置参数共享利用参数存在大量冗余的特点，目的都是为了减少参数数量，达到减少运算量去除冗余的目的。）