条件DDPM:Diffusion Model的第三个巅峰之作

2023-11-20

字数统计: 1.4k字 | 阅读时长≈ 5分

条件DDPM:Diffusion Model的第三个巅峰之作

前言：DDPM2020年诞生，短短一年的时间，模型上有两个巨大的改进，其中一个就是condition的引入，很多后续DDPM相关的论文都会讨论这一点，有些文章称之为latent variable。和当年GAN的发展类似，CGAN和DCGAN的出现极大程度上促进了GAN的发扬光大，意义重大。本文基于前面几篇文章继续聊一聊:

诞生之初：unconditional无条件生成

论文：Denoising Diffusion Probabilistic Models

根据郎之万动力方程的推导，最终的生成表达式中依赖神经网络对噪声的预测可以生成图像，但是这种生成是没有任何约束的，也就是说给定纯高斯噪声，我们就能生成图片。好处是我们的输入不受任何控制，只要是高斯噪声就可以，坏处是我们无法监督这一过程，最终生成的结果不受控制。比如在SUN数据集上，我们能任意生成各种各样的图像:

首次引入condition：分类器指导

论文：Diffusion Models Beat GANs on Image Synthesis

在上一篇文章发表几个月之后，第一个condition DDPM诞生了。这篇文章在lmageNet上训练了一个分类器，用这个分类器控制标签。这个分类器是unet结构，带有attention pool，添加随机crops减少过拟合。

用 $y$ 表示标签，$p_{\phi}\left( y|x_t,t \right)$ 代表分类器，使用梯度 ${x_t}log p{}( y|x_t,t ) $ 来指导扩散过程朝向任意类别标签 $y$ 发展。简而言之，将类信息合并到规范化层中，利用分类器$p_{\phi}\left( y|x_t,t \right)$改进生成器。

反向sample过程中，在 $x_{t+1}$ 和 $y$ 条件下生成 $x_t$ ，可以写成以下式子： \[ p_{\theta ,\phi}\left( x_t|x_{t+1},y \right) =Zp_{\theta}\left( x_t|x_{t+1} \right) p_{\phi}\left( y|x_t \right) \] 其中大写的 $Z$ 是一个常数，文章里详细证明了这个公式成立。其中 $p_{\theta}( x_t|x_{t+1})$ 和 unconditional DDPM是一样的，因此只多了 $p_{\phi}\left( y|x_t \right)$ 这一项。

同时这篇文章还重点探索了一个缩放因子 $s$ 的作用，缩放因子放缩的是分类器梯度 $\sum{\nabla _{x_t}\,\,\log p_{\phi}\left( y|x_t,t \right)}$ 之和，实验表明缩放因子越大，重建出来的FID越小，即重建质量越高。

开源的代码如下：

def cond_fn(x, t, y=None):
    assert y is not None
    with th.enable_grad():
        x_in = x.detach().requires_grad_(True)
        logits = classifier(x_in, t)
        log_probs = F.log_softmax(logits, dim=-1)
        selected = log_probs[range(len(logits)), y.view(-1)]
        return th.autograd.grad(selected.sum(), x_in)[0] * args.classifier_scale

发扬光大：sample全程加入参考图片

论文：ILVR:Conditioning Method for Denoising Diffusion Probabilistic Models

时间来到一年后，一篇ICCV上的oral论文重点讨论了一种conditional方式，在sample过程中加入参考 图片，引导重建的图像和参考图像相似。

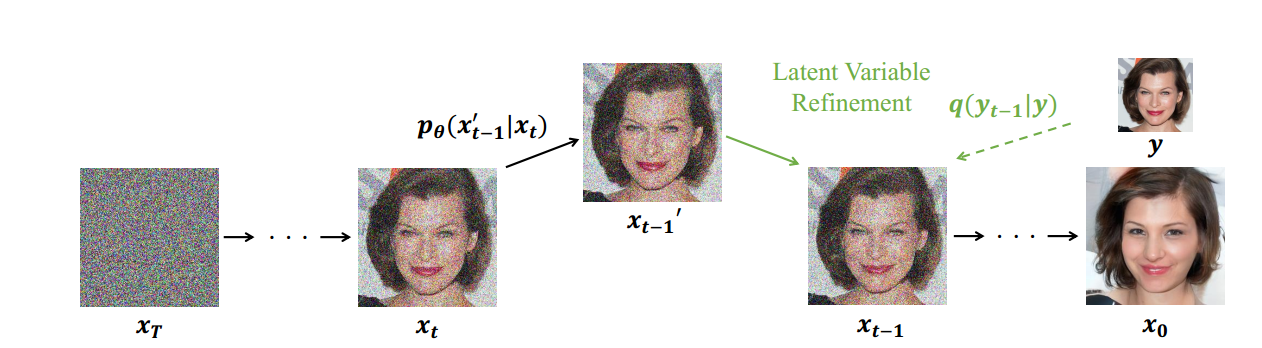
这就不仅仅是标签/类别控制了，从某种意义上来说，我们能控制生成的风格，这样DDPM就能和GAN 样，完成图像修复、P图、风格迁移甚至多模态等任务!

参考图片定义为 $y$ 。现在我们需要再条件 $c$ 和 $x_t$ 推导 $x_{t-1}$ ， $\phi _N$ 表示一个低通滤波器，这个低通滤波器可以是 Bilinear、Lanczos3、Lanczos2、Bicubic 等，这个低通滤波器的作用是确保生成图像和参考图像在低通维度信息上接近，条件 $c$ 用来确保生成图像 $\phi _N(x_0)$ 和参考图像 $\phi _N(y)$ 相等，因此方程式可以写成： \[ p_{\theta}\left( x_{t-1}|x_t,c \right) \approx p_{\theta}\left( x_{t-1}|x_t,\phi _N\left( x_{t-1} \right) =\phi _N\left( y_{t-1} \right) \right) \] \[ x_{t-1}^{'}~p_{\theta}\left( x_{t-1}^{'}|x_t \right) \] \[ x_{t-1}=\phi \left( y_{t-1} \right) +\left( I-\phi \right) \left( x_{t-1}^{'} \right) \]

再次，我们将condition部分和uncondition的部分分开了，这篇论文重点探究了downsampling $N$ 因子对实验的影响，设 $\mu$ 是无条件DDPM生成集合，这个集合的特点：

参考图像选择的最小要求
参考有向子集的用户可控性，定义了参考图像的语义相似度

随着因子N的增加，可以从更广的图像集合中进行采样，采样后的图像更加多样化，与参考图像的语义相似度也更低。与参考图像的感知相似度是有下采样因子控制的，高因子 $N$ 的样本具有参考样本的粗特征，而低因子 $N$ 的样本也具有参考样本的特征。

看一下代码，这个 $N$ 实际上就是一个resize系数：

1 2	down = Resizer(shape, 1 / args.down_N).to(next(model.parameters()).device) up = Resizer(shape_d, args.down_N).to(next(model.parameters()).device)

这个resize操作来自：

https://github.com/assafshocher/resizer

这个作者真牛逼，仅仅对做一个resize操作来研究sanple的性质。

流水线式创新：潜在变量约束

在得到前文的思路启发之后，此类文章如雨后春笋式量产，不乏CVPR Oral这样的好文章，比如这篇文章：

论文：Diffusion Probabilistic Models for 3D Point Cloud Generation

结尾

Condition的引入是DDPM的一个重大突破，现在已经被广泛运用在DDPM论文中。

DDPM有一个致命的问题，就是运算量过大，采样时间过长，如何加速？后面再聊。

本文作者： 李宝璐
本文链接： https://libaolu312.github.io/2023/11/20/条件DDPM-Diffusion-Model的第三个巅峰之作/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！