从DDPM到DDIM:Denoising Diffusion Implicit Models

前言：DDIM发表在LCRL2021上，是DDPM重要的改进之一，能显著提高DDPM的样本质量、减少采样时间，并且已经被广泛应在到现在的Diffusion Models上。

目标：消除DDPM与GAN之间的效率差距

一句话概括：剪短前向，进而使逆向更简单，其实DDIM就是一种新的采样方式，剩下的部分还是DDPM的东西。

DDPM的缺点：多次迭代耗时耗力

DDPM需要许多迭代来产生高质量的样本。例如在一块NVIDIA 2080Ti GPU上生成50k张32*32的图片，DDPM需要20小时，GANs只需要不到一分钟。因为对于DDPM来说，生成过程(从噪声到数据)可能有数千个步骤；需要迭代所有步骤来生成单个样本，而GANs只需要通过一次网络，一步就能生成。

超参数T的作用和限制

前向过程的timesteps T是DDPM中一个重要的超参数。从变分的角度来看，较大的T可以使反向过程接近高斯分布(Sohl-Dicktein et al.2015)，因此用高斯条件分布建模的生成过程成为很好的近似；这促使人们选择较大的T值。

然而，由于所有的T迭代都必须按顺序而不是并行执行，以获得一个样本\(x_0\)，从DDPM中采样比从其他深度生成模型中采样要慢得多，这使得它们在计算有限和延迟关键的任务中不切实际。

话不多说，直接上手写版：

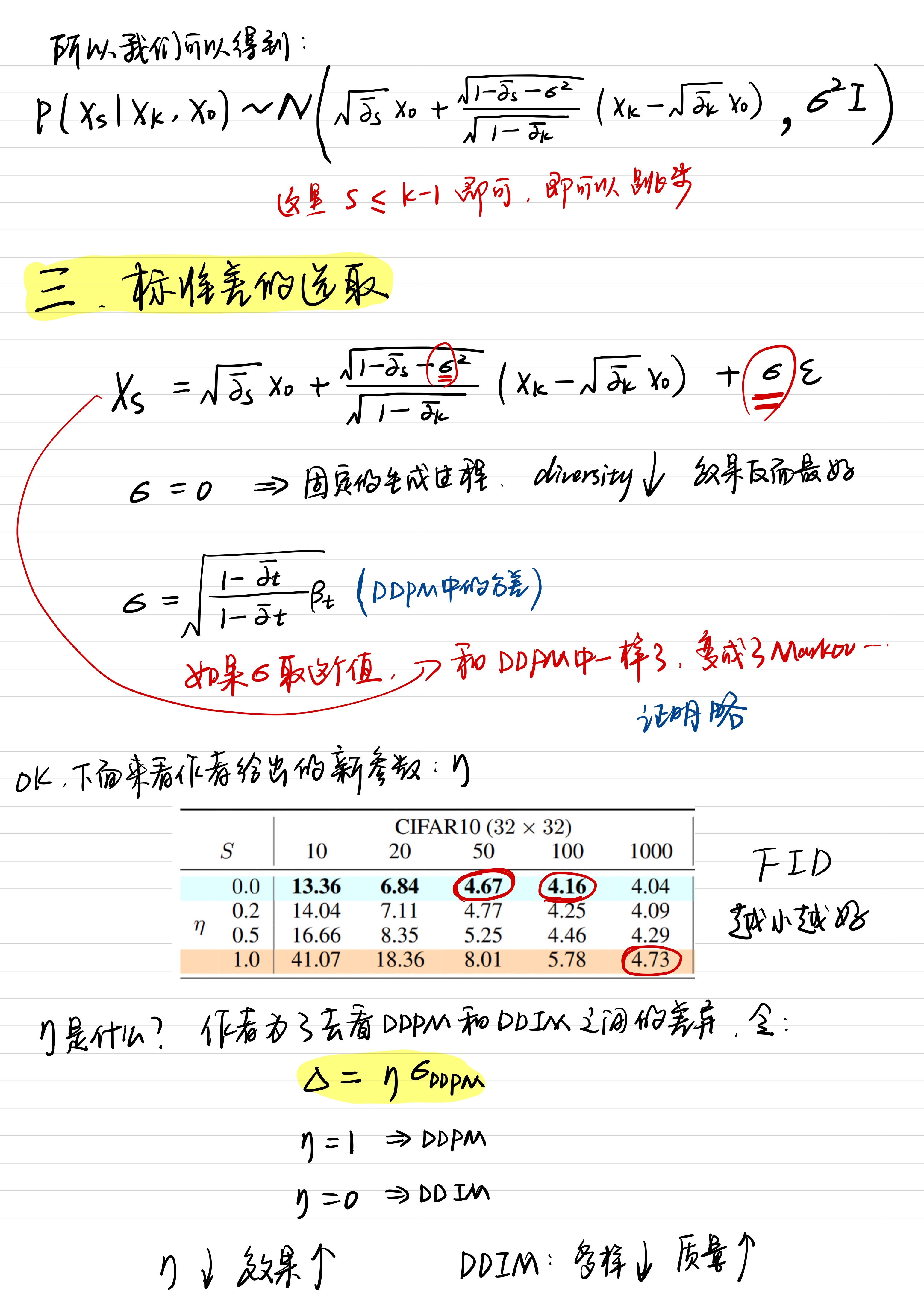
OK，到这里为止，DDIM的数学原理和效果已经解释的很清楚了，下买还是分模块的细化一下。

非马尔科夫正向过程的变分推断

我们知道在DDPM中前向过程是一个马尔科夫过程，具有无记忆性，这一点在DDPM论文中有详细证明。

DDIM对于非马尔科夫过程，设计出合适的反向生成马尔科夫链。产生的变分训练目标有一个共享的替代目标，这正是用于训练DDPM的目标。能够使用非马尔科夫扩散过程，这导致了短的可生成马尔科夫链，可以在少量步骤中模拟。这只会在样本质量略微降低的情况下，极大地提高采样(生成样本)的效率。

非马尔科夫前向过程（没什么用）

先考虑推理分布，用 \(q_{\sigma}\left( x_{1:T}|x_0 \right) :=q_{\sigma}\left( x_T|x_0 \right) \prod_{t=2}^T{q_{\sigma}\left( x_{t-1}|x_t,x_0 \right)}\) 表示，其中 \(q_{\sigma}\left( x_T|x_0 \right) =\mathcal{N}\left( \sqrt{\alpha _T}x_0,\left( 1-\alpha _T \right) I \right)\) 是高斯分布。

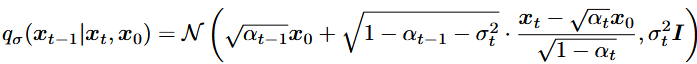
选取均值函数进行排序以保证 \(q_{\sigma}\left( x_T|x_0 \right) =\mathcal{N}\left( \sqrt{\alpha _T}x_0,\left( 1-\alpha _T \right) I \right)\) 对于所有 \(t\) 都成立。因此定义了一个联合推断分布，它与边缘分布想匹配，正向过程可以从贝叶斯规则导出： \[ q_{\sigma}\left( x_t|x_{t-1},x_0 \right) =\frac{q_{\sigma}\left( x_{t-1}|x_t,x_0 \right) q_{\sigma}\left( x_t|x_0 \right)}{q_{\sigma}\left( x_{t-1}|x_0 \right)} \] 所以这里的正向过程不再是马尔科夫过程，因为每个 \(x_T\) 都可以依赖于 \(x_{t-1}\) 和 \(x_0\) 。\(\sigma\) 的大小控制着正向过程的随机程度；当\(\sigma->0\) ，我们得到了一个极端的情况，只要我们观察某个 \(t\) 的 \(x_0\) 和 \(x_t\) ，那么 \(x_{t-1}\) 是已知且固定的。

论文中这一节的内容，旨在抛砖引玉，其实在DDIM中并没有用到这部分的东西，但是这样的前向扩散过程就不再是一个马尔科夫过程。

生成过程

定义一个可训练的生成过程 \(p_{\theta}\left( x_{0:T} \right)\) ，每一个生成过程 \(p_{\theta}^{\left( t \right)}\left( x_{t-1}|x_t \right)\) ，原先得到 \(x_t\) 的公式是： \(x_t=\sqrt{\alpha _t}x_0+\sqrt{1-\alpha _t}\epsilon\) ，重写这个方程，用神经网络 \(\epsilon _{\theta}^{\left( t \right)}\left( \alpha _t \right)\) 从 \(x_t\) 预测出 \(\epsilon_t\) :

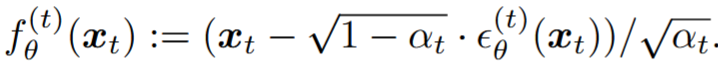
固定先验 \(p_{\theta}\left( x_t \right) =\mathcal{N}\left( 0,I \right)\) ，生成过程可以定义为：

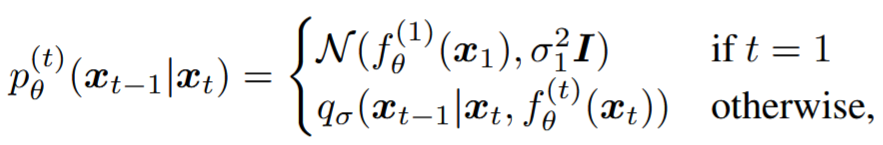
统一变分推理目标

通过下面的变分推理目标优化 \(\theta\) ：

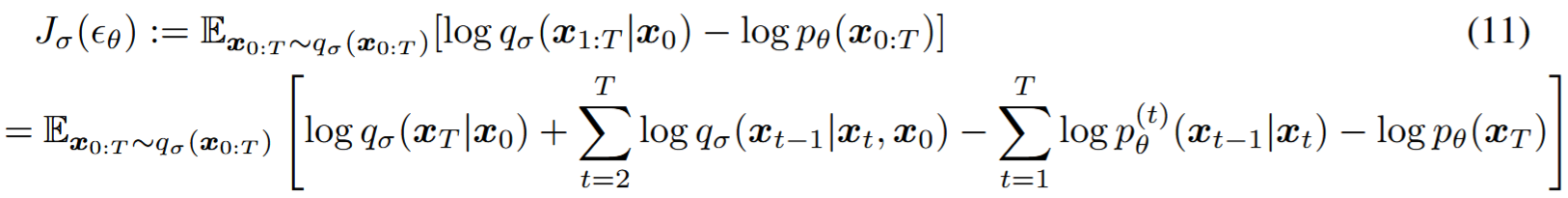
不同的模型必须训练对应的 \(\sigma\) ，因为它对应着不同的变分目标和不同的生成过程。

对于特定的权重 \(\gamma\) ，\(J_{\sigma}\) 恒等于变分目标 \(L_{\gamma}\) 加常数，即 \(J_{\sigma}=L_{\gamma}+C\)。（定理1）

变分目标 \(L_{\gamma}\) 是特殊的，因为如果模型 \(\epsilon _{\theta}^{\left( t \right)}\left( \alpha _t \right)\) 的参数 θ 在不同的 t 之间不共享，那么θ的最优解将不取决于权重 \(\gamma\)（因为全局最优是通过分别最大化和中的每个项来实现的）。

\(L_{\gamma}\) 的这个性质有两个含义：一方面，这证明使用 \(L_{1}\) 作为DDPM中变分下界的替代目标函数是合理的；另一方面因为 \(J_{\sigma}\) 等价于定理1中的一些 \(L_{\gamma}\) ，因此 \(J_{\sigma}\) 的最优解也与 \(L_{1}\) 的最优解相同。

因此，如果模型θ中的参数不在t之间共享，那么 \(L_{1}\) 目标也可以用作变分目标 \(J_{\sigma}\) 的替代目标

采样过程

我们可以使用预训练的DDPM作为新目标的解决方案，并专注于寻找一个生成过程，通过改变 \(\sigma\)，可以更好地生成出符合我们需求的样本。

去噪扩散隐式模型（上面的手写推导）

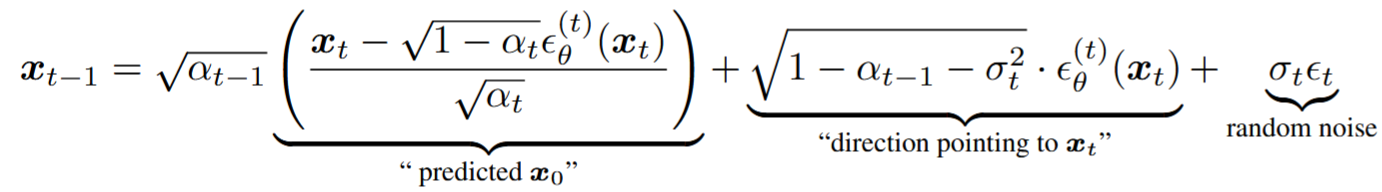
DDIM的 \(x_{t-1}\) 公式写成：

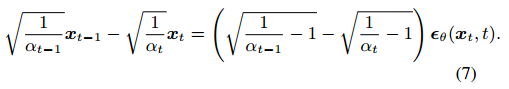
加速生成过程

上面分析过，这里就不做赘述

显示控制插值

当考虑较少的迭代时，DDIM在图像生成方面优于DDPM，其速度比原始DDPM生成过程提高了10到100倍。而且，与DDPM不同的是，一旦初始潜在变量 \(X_T\) 是固定的，无论生成轨迹如何，DDIM都能保持图像的高级特征，因此可以直接从潜在空间进行插值。DDIM还可以用于从潜在代码中重构样本的编码，这是由于随机抽样过程，DDPM是无法做到的。

后面有时间会专门写一个做插值的文章。